Why I'm wrong?

Calvin Edit: Discussion about mistakes made in a problem should occur on the solution discussion, so that others who work on the problem can also learn from it. I have locked this discussion.

In Parth Lohomi's question

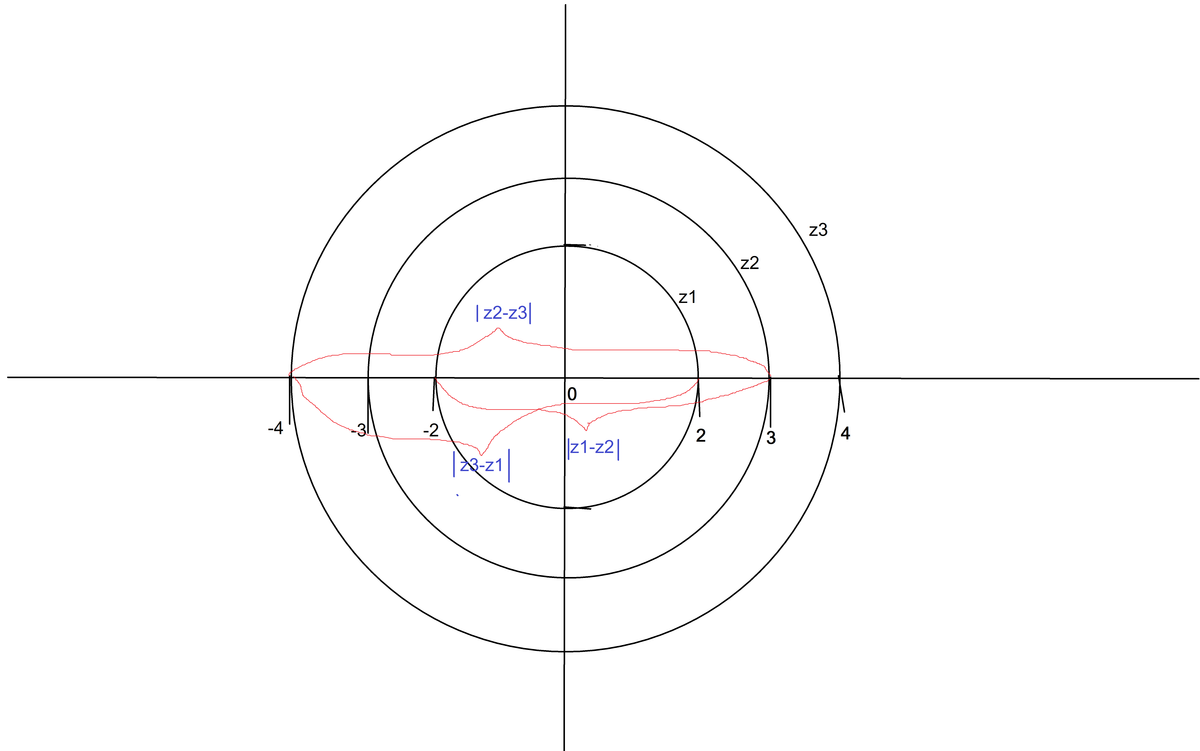
It is given $\left| { z }_{ 1 } \right| =2,\left| { z }_{ 2 } \right| =3\quad and\quad \left| { z }_{ 3 } \right| =4$ and we have to find the maximum value of $|z_1-z_2|^2 + |z_2-z_3|^2 + |z_3-z_1|^2$ .

here is how I did the problem,

We know that $\left| { z }_{ 1 } \right| =2$ represent a circle with center (0,0) and radius=2. Similarly $\left| { z }_{ 2 } \right| =3$ and $\left| { z }_{ 3 } \right| =4$ represent circles with radius 3 and 4 respectively and centers (0,0)

Now drawing these circles on complex plane we get maximum values of,

$\left| { z }_{ 1 }-{ z }_{ 2 } \right| =5\Longrightarrow { \left| { z }_{ 1 }-{ z }_{ 2 } \right| }^{ 2 }=25$

$\left| { z }_{ 2 }-{ z }_{ 3 } \right| =7\Longrightarrow { \left| { z }_{ 2 }-{ z }_{ 3 } \right| }^{ 2 }=49$

$\left| { z }_{ 3 }-{ z }_{ 1 } \right| =6\Longrightarrow { \left| { z }_{ 3 }-{ z }_{ 1 } \right| }^{ 2 }=36$

Therefore $|z_1-z_2|^2 + |z_2-z_3|^2 + |z_3-z_1|^2$ =25+49+36=110

But this answer is shown wrong......So what has I done wrong in solving this?Please help.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the “dot dot dot” menu in the lower right corner. You will get a more timely response that way.

This also allows those who have made a similar error to learn from your experience.

Calvin Lin Staff - 6 years, 3 months ago

Ok, Thanks sir

Anandhu Raj - 6 years, 3 months ago

@Calvin Lin , @Parth Lohomi @Swananda Punde , , @Deepanshu Gupta, @Ronak Agarwal Could you help please...

Anandhu Raj , it is true that these are the maximum values of the expressions $|z_1 - z_2| \dots$ , but these are not simultaneously satisfied for any triplet. To make my point clearer and simple to understand consider any point $z_1$ and find the corresponding $z_2$ so that $| z_1 - z_2 |$ is $5$ . Similarly, find a $z_3$ for the previously found $z_2$ so that $| z_2 - z_3 | = 7$ . Now you have all the three points $z_1$ , $z_2$ and $z_3$ . Is $| z_1 - z_3 | = 6$ ?

Sudeep Salgia - 6 years, 3 months ago

Oh! got it ..Thanks! So is there any geometrical approach for this question?

@Unnikuttan Cheranalloor The equation ${ (x-3) }^{ 9 }+{ (x-{ 3 }^{ 2 }) }^{ 9 }+{ (x-{ 3 }^{ 3 }) }^{ 9 }+..........+{ (x-{ 3 }^{ 9 }) }^{ 9 }=0$ has

(a) all the roots real.

(b)1 real and 8 imaginary roots.

(c)real roots namely x= $3,{ 3 }^{ 2 },{ 3 }^{ 3 }.....{3}^{9}$

(d)5 real and 4 imaginary roots.

How to do?

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$