Trigonometry! #9
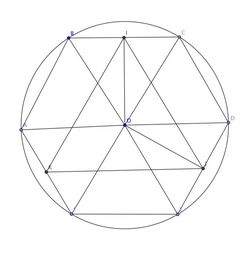 Hexagon
A
B
C
D
E
F
is inscribed in the circle of radius
R
.
A
B
=
C
D
=
E
F
=
R
. Points
I
,
J
,
K
are the midpoints of segments
B
C
,
D
E
,
F
A
respectively. Then
Δ
I
J
K
is:
Hexagon
A
B
C
D
E
F
is inscribed in the circle of radius
R
.
A
B
=
C
D
=
E
F
=
R
. Points
I
,
J
,
K
are the midpoints of segments
B
C
,
D
E
,
F
A
respectively. Then
Δ
I
J
K
is:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Try using complex numbers to approach this problem!
I will try , but I did it in other way ,
Take O coordinates as (0,0) and other as (a,b) , now by quadrants the coordinates signs will change and then applying mid point formula we can find the coordinates of the vertices of the triangle , and we can see that each side length is equal so equilateral or we can say that all the three coincide at one point , thus equilateral
Vectors and complex numbers would often offer easier bookkeeping, especially since there is so much rotation around.
Let the points be on the unit circle, with A = α , C = β , E = γ . Since A B = C D = E F = r , we can treat B , D , F as rotation of A , C , E by the 6 0 ∘ = ω , where ω 6 = 1 . Thus B = α ω , D = β ω , F = γ ω .
Then, I is the midpoint of B C , so its represented by 2 α ω + β . Likewise, K = 2 γ ω + α and J = 2 β ω + γ .
Now, we get that K I = I − K = 2 α ( ω − 1 ) + β − γ ω and likewise I J = 2 − α ω + β ( ω − 1 ) + γ .
We can now easily verify that ω 2 K I = I J which tells us that they are equal length, and meet at an angle of 2 × 6 0 ∘ . Thus, we have an equilateral triangle.
Those sides that are equal makes the six triangles to be congruent, so it is a regular hexagon, and the asked triangle is equilateral
This is how far I got. Note that I've taken ∠ I O C = ∠ I O B = u , ∠ J O D = ∠ J O E = v , ∠ K O A = ∠ K O F = w .
The method given to me is to find O I and O J . Then using cosine rule, in Δ O I J I had to find I J and then simplify it until it becomes symmetrical in u , v and w and R . Then we can say that the triangle is equilateral.
I got O I = R cos ( u ) and O J = R cos ( v ) . Also, in Δ O I J , ∠ I O J = 6 0 ∘ + u + v . So using cosine rule, I J 2 = R 2 cos 2 ( u ) + R 2 cos 2 ( v ) − 2 ( R cos ( u ) ) ( R cos ( v ) ) ( cos ( 6 0 ∘ + u + v ) ) ahead of which I don't know what to do. I need to make this expression symmetrical in u , v and w and R . A helpful point is that u + v + w = 9 0 ∘ . I don't know how to use it. Help would be appreciated. Thanks! :)