Plenty of dots
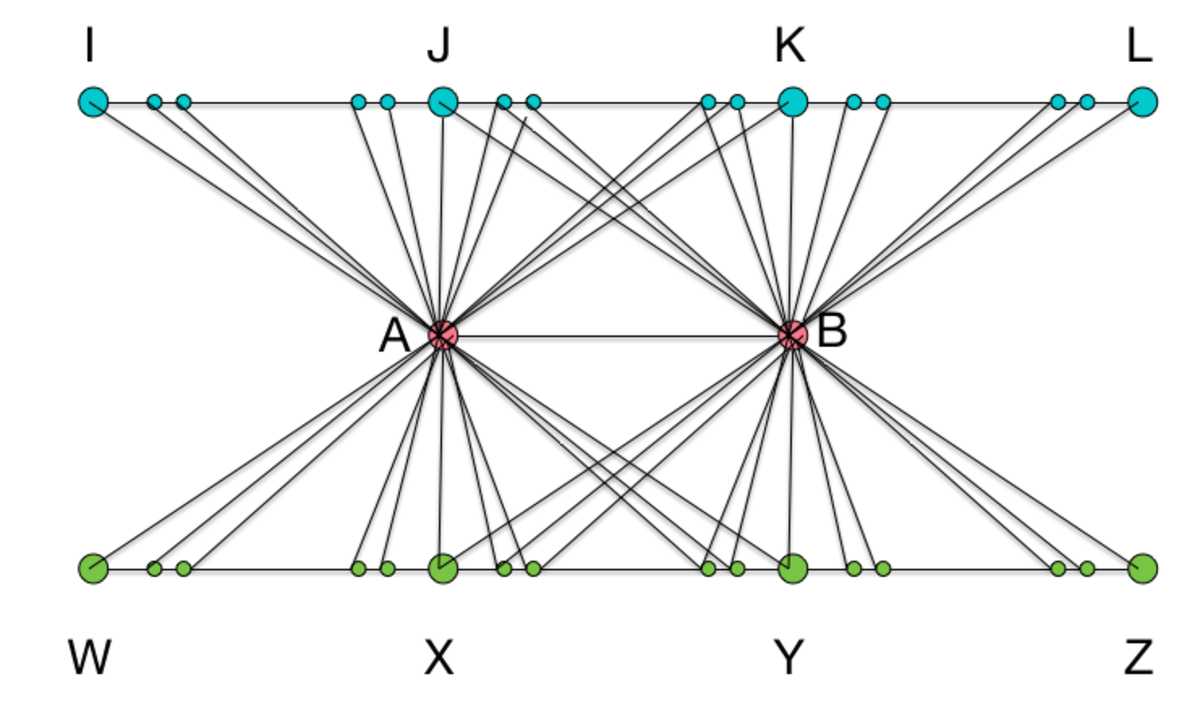
Find the number of quadrilaterals in the given figure. Do not include degenerate quadrilaterals.
In the given figure, IJKL, AB & WXYZ are line segments that are parallel to each other.
There are 20 defined points on IJ which are connected to A by line segments.
There are 20 defined points on JK which are connected to both A and B by line segments.
There are 20 defined points on KL which are connected to B by line segments.
There are 20 defined points on XW which are connected to A by line segments.
There are 20 defined points on XY which are connected to both A and B by line segments.
There are 20 defined points on YZ which are connected to B by line segments.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
So, for two 4 1 q u a d r i l a t e r a l s on the same base, the number of quadrilaterals are 1 6 8 1 ∗ 2 = 3 3 6 2
Now, the number of quadrilaterals in the middle region is twice the square of the triangles in any one part (upper part or lower part)
So, counting in this manner the number of triangles in 20 triangles on the same base are
2
8
7
0
So, number of quadrilaterals in the middle region is
1
6
4
7
3
8
0
0
Now, there are
6
6
2
2
points in the middle region, that are not counted because of the presence of any extra
r
e
c
t
a
n
g
l
e
. Now,
2
1
6
0
1
quadrilaterals have not been counted due to the presence of following such figures.
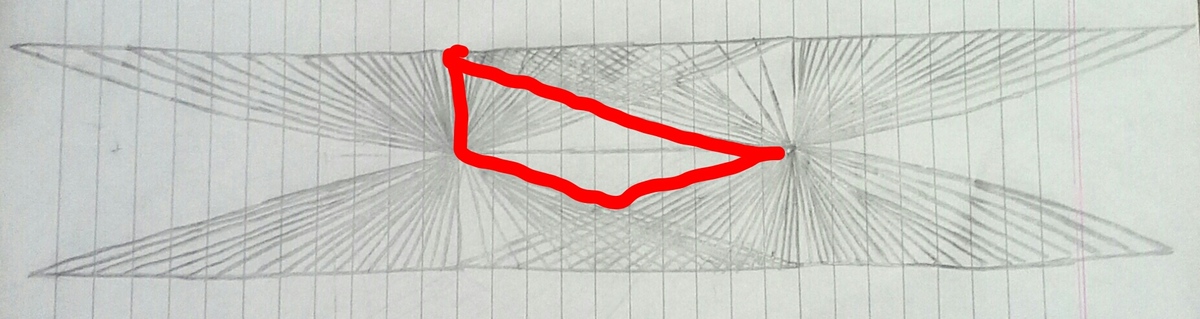
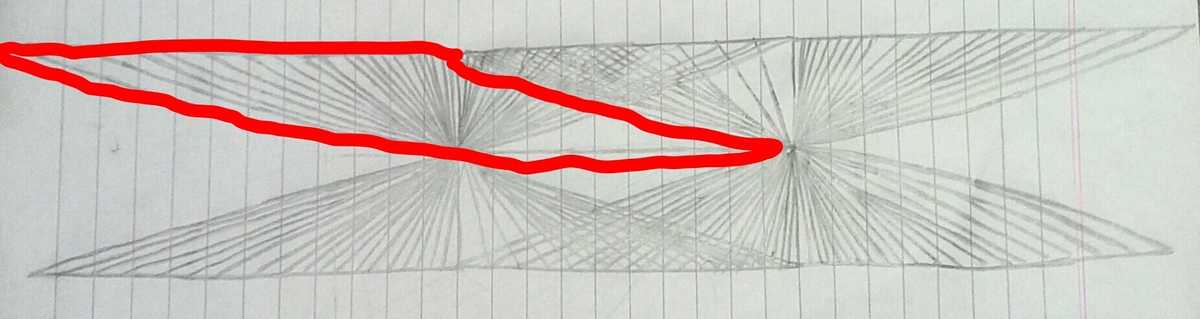
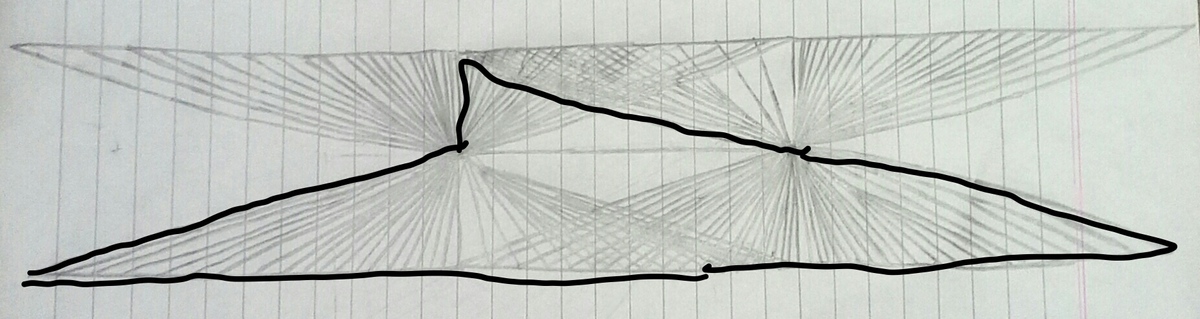
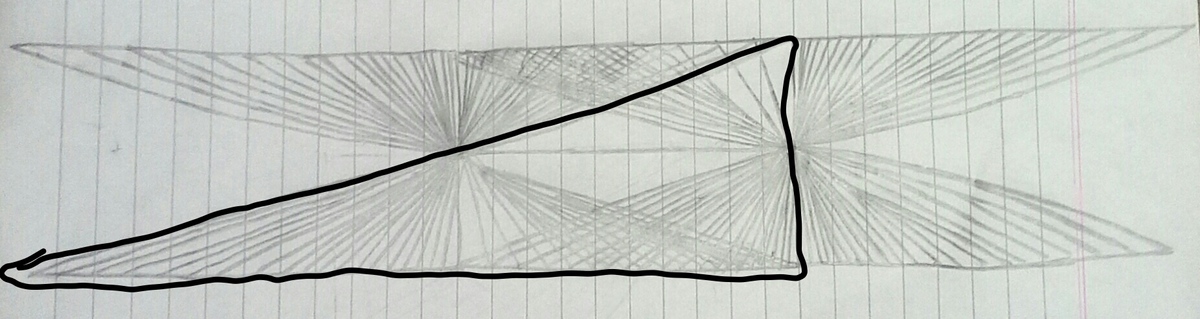
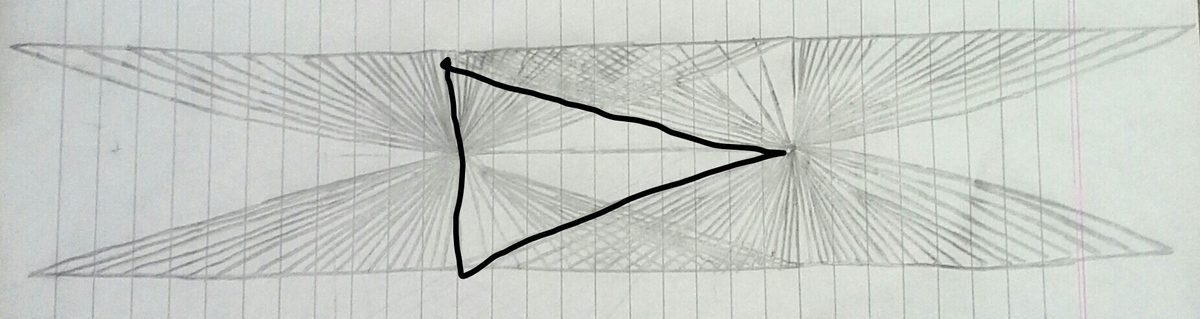
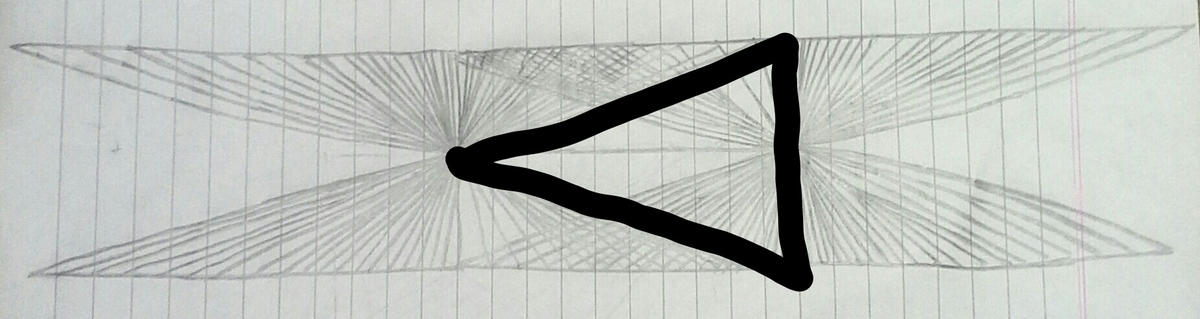
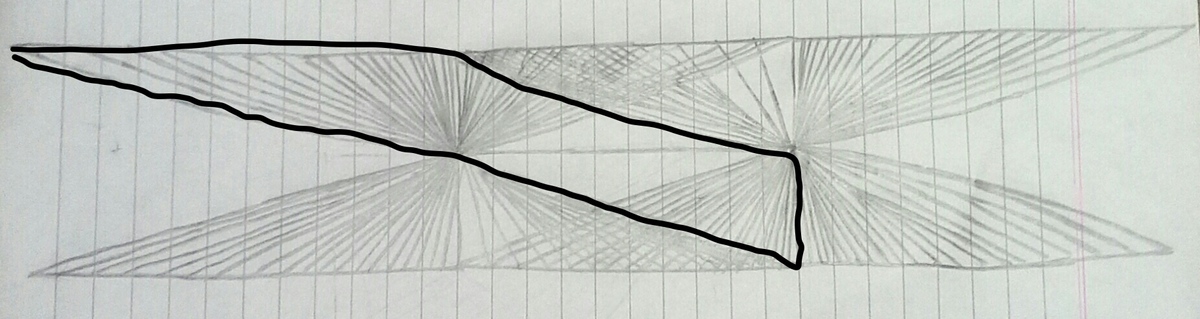Now, the following six figures have to be excluded, because they are triangles.
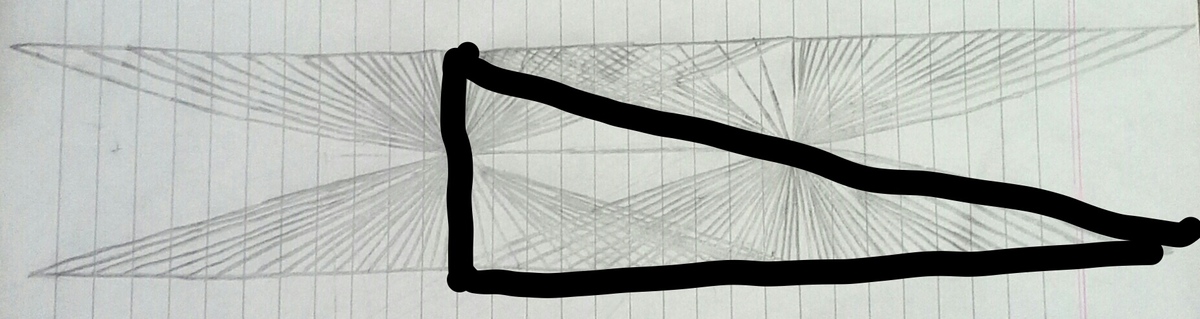
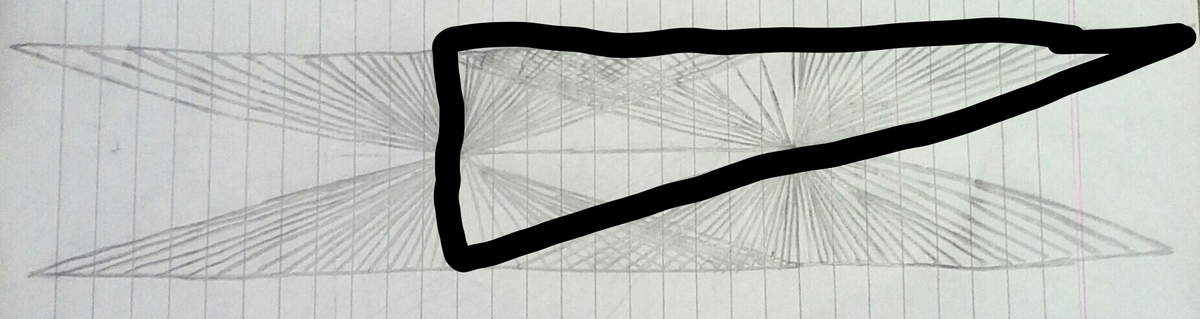
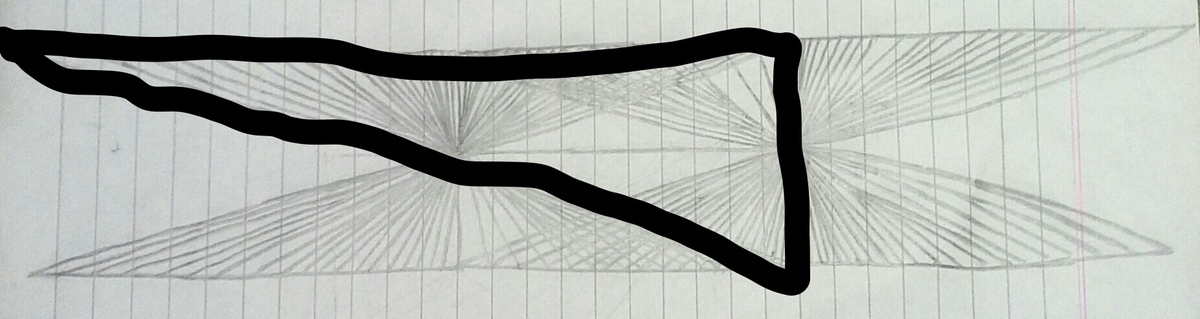So, the total number of quadrilaterals in the given figure(question) =
[
3
3
6
2
+
1
6
4
7
3
8
0
0
+
6
6
2
2
+
2
1
0
6
1
]
−
6
=
1
6
5
0
5
3
8
5
−
6
=
1
6
5
0
5
3
7
9
Hope you like my solution