1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, ...

Without having the nature of the sequence explicitly stated we must make an assumption about its behavior. It seems reasonable to assume that the sequence is made up of one 1, two 2's, three 3's, and so on. If the sequence continued up to the last n, there would be $1 + 2 + ... + n$ = $\frac{1}{2}n(n+1)$ terms.

• We can verify that, $\frac{1}{2} × 44 × 45 = 990$ . In other words, the 990th term is the last 44, the next 45 terms will be 45, hence the 1000th term must be $\boxed{45}$

i simply start adding the terms on calculator

1

22

333

4444

55555

666666 on this pattern .(n(n+1))/2) . according to this law for the value of n=10, we find the the value of term is55. where 10 is the last term of series 10. for n=44 we see the value of full term is 990.where 44 is the last term of series no 44. so definitely 45 is the 1000term of next.that means series of 45.

Ceiling function of square root of (2000-1)

You can use integrals.

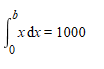
Solve this equation for b to find the x value in which the area under the graph is 1000. This works because the area under the graph=number of terms used and x values=the term itself. I used maple because I am lazy:

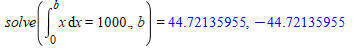
Of course, the pattern doesn't allow negative values so we will ignore that. WIth the area under the graph=1000 in the x value 44.7, we can just round up to find the correct value, which is 45.

The series is 1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6,6,6... here 1-repeats constantly till term 1(0+1)
2-repeats constantly till term 3(1+2)
3 3 3-repeats constantly till term 6(1+2+3) 4 4 4 4-repeats constantly till term 10(1+2+3+4) ... Here observe that if a no. x is of the form 1+2+3+4+5...+n=x, then n repeats n times constantly till the term x.Think that x is a no. just below 1000.Then n repeats itself constantly till term x. Using equation n(n+1)/2=1000 we see n=44 and x=990.Now it is easy to note that 45 starts repeating after the 990th term and that the 1000th term is 45.

Lets assume that the no. of terms is the sum of the sequence, because as you can see the number is repeated according to itself so we can assume that the sum of the sequence is 1000. Using n(n+1)/2 we can equal it to 1000. n(n+1)/2=1000 --- n2+n=1000(2) --- n2+n=2000 ---- n2+n-2000=0 using quadratic formula we get 44.5 and 45.5, in the sequence we can see that its not in decimal form so lets just remove the decimal that makes it 44 and 45. Second lets check if 44 or 45 satisfy.Using n(n+1)/2 first using 44 --- 44(44+1)/2= 44(45)/2= 990 meaning the number 44 ends in 990th term meaning that 45 has the bigger chance. Using 45 ---- 45(45+1)/2=45(46)/2= 1035 meaning the term 45 starts in 936th term and it ends in 1035th term so the answer is 45 hope it helps

From what we're given, we can deduce that the end-index of a certain number $x$ can be given as $\sum_{n=1}^x n$ . To solve for the 1000th term, we just need to find the first intenger that satisfies the equation $\sum_{n=1}^x n \geq 1000$ . 44 does not, as the summation of natural numbers 1-44 is 990. $990+45=1035$ , so $\boxed{45}$ must be the answer.

$1+2+3+. . .+44=990$ $\Rightarrow$ $1,2,2,3,3,3,4,4,4,4,. . .,44,44,44,44,44,44,44, . . ., 44$ (total 990 numbers) $, 45,45,45,45,45,45,45,45,45,\boxed{45}$ .

Just Use the formula of natural number n(n+1)/2..

In the sequence, the number 1 has 1 time, number 2 has 2 times, number 3 has 3 times, number 'n' has 'n' times. So 'n' is from (((n-1)*n)/2)+1 to (n(n+1)/2 terms...

If we took (((n-1)*n)/2)+1 = 1000

then, n = 45.something

So 1000 term is in the consecutive line of 45

So the answer is 45...

Bcoz numbers r repeated according to their value i.e 1 is 1 times 2 is 2 times , 3 is 3 times , so to find thousandth term we need to find that term of series where the sum becomes approximately equal to 1000

so by sum of n terms formula in arithmetic progression 1000~ n/2(2a+(n-1)*1) or simply 1000= n(n+1)/2 or n~45 nd 44 approx no since series is ongoing so 45 will eb repeated 45 times nd in that sum 1000 would hav been completed so 45 is the right answer

thank you

1,2,2,3,3,3,4,4,4,4,5,5...... So It is an AP 1,2,3,4,5,6.......... Now by Hit and Trial We get that sum of 45 terms of this AP is 1035 Required term is 1000 Subtracting 1000 from 1035 we get 35 so we know that 45th term is repeated 45 times so as diff. is 35 so 1000th term will be 45

1,2,2,3,3,3,4,4,4,4...----------(a) this series can written as One+Two+Three+Four+Five.....----(b) ("Two" means in equation (b) is 2 has came 2 times in equation ( a). similarly "three" means in equation (b) is 3 has come 3 times in equation ( a) so we want 1000 term it means sn=1000 in modified equation(b) means 1000 term in equation (a)

Sn=1000 a=1 d=1 n=??? ( from equation b) (n/2)*(2a(n-1)d, after simplification n^2=2000 n=44.72~~45 so n=45

There are 1 value with the value of 1 There are 2 values with the value of 2 ETC... 2's are from terms 2 - 3 all the numbers before the first 3 is 1, 2, 2, so 3 starts after 1+2 5's are from terms 11 - 15 all the #s before 6 is 1,2,2,3,3,3,4,4,4,4,5,5,5,5,5, so 6 strats after 1+2+3+4+5 or 15 terms.

If you add all the integers up to 45, you would get pass 1000 or 1035 to be exact. the value 45 stops at the 1035th term

If only add up to 44, you get 990.And the value 44 stops at the 990th term 1000 is between 990 and 1035 Therefore the 1000th term is 45, (because it's over 990)

consider the sum of 1st,3rd,6th........... number of this series
therefore we have the inequation n(n+1)/2<1000 find the largest possible value for n and then add 1

[n(n+1)]/2

Putting up the values, you will get the answer. Obviously approx.

=(45*46)/2

=2070/2

=1035

We get 1035 which means that 45 will go on till 1035th term and the asked term is 1000.

Therefore, the required answer is 45.

$\frac{n(n+1)}{2}=1000$

$\boxed{n=45}$