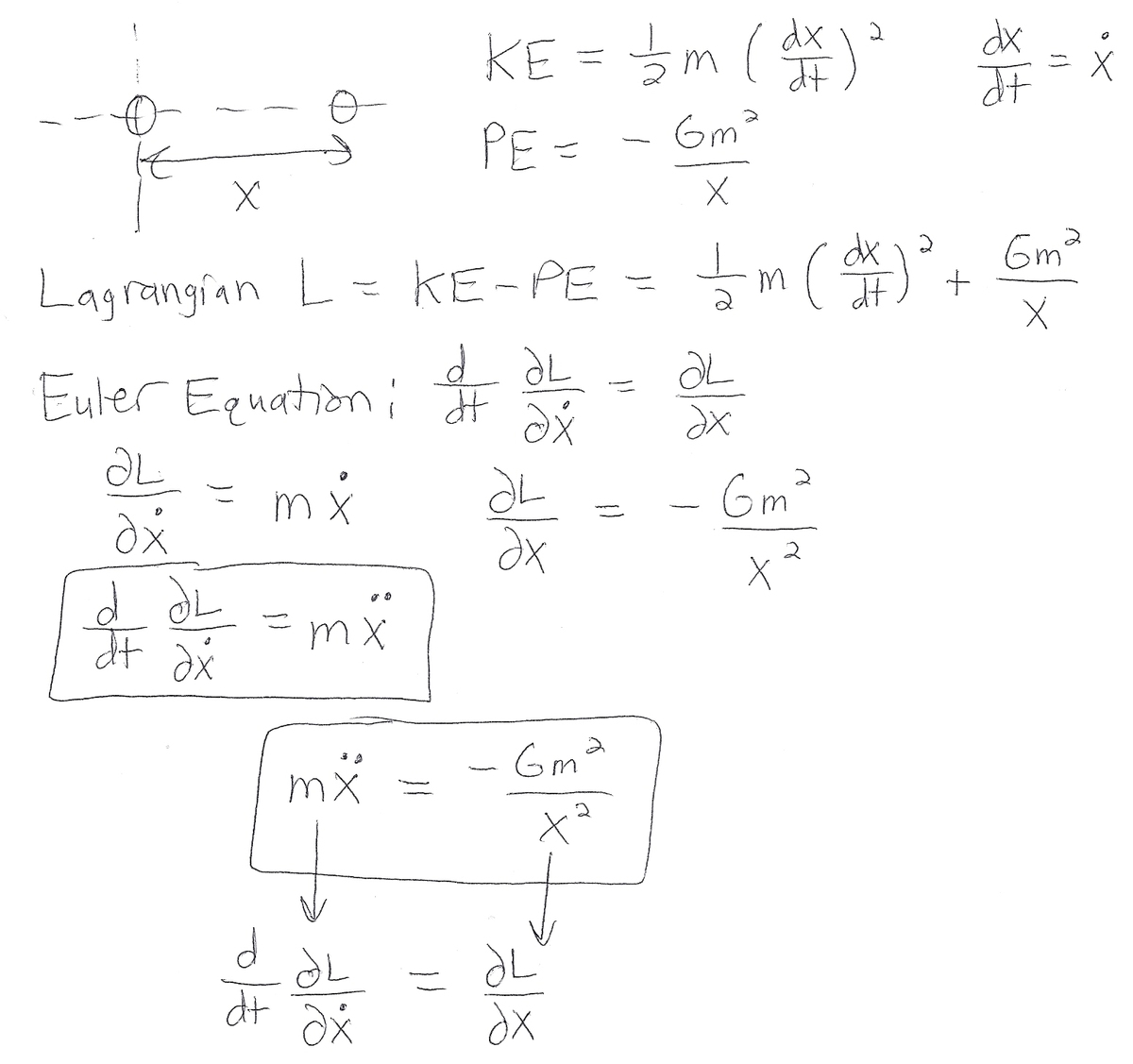
1-D Lagrangian Mechanics

Classical Mechanics Level 3

Consider a simple 1-D system consisting of two identical massive particles (with mass $m$ ). One is fixed at the origin, and the other is free to move and is located a distance $+x$ from the origin.

If each particle only experiences the gravity force from the other particle, the differential equation describing the moving particle's position is:

$\Large{m \ddot{x} = \frac{-G m^{2}}{x^{2}}}$

We can derive this expression by formulating the behavior of the system in terms of Lagrangian mechanics . In that case, which part of the Euler equation does the $\large{m \ddot{x}}$ term correspond to?

Notes: The dot notation denotes time-differentiation. The term $L$ represents the Lagrangian of the system. The term $G$ is the universal gravitational constant.

{\frac{\partial L}{\partial x}}

{\frac{\partial^{2} L}{\partial t^{2}}}

{\frac{d}{dx}\frac{\partial L}{\partial t}}

{\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}}

1 solution

Steven Chase
Dec 13, 2016

1-D Lagrangian Mechanics

1 solution

0 pending reports