1 LAKH POINTS PROBLEM!!!!

Classical Mechanics Level 5

A transparent sphere of radius $R$ and refractive index $n$ is at rest on a horizontal surface.A ray of light is incident parallel to the vertical diameter and at a distance $d$ from it.Let $n$ be in range ( $\alpha$ , $\beta$ ].Find $\alpha+\beta$ . Assume: The rays intersects the diameter at the point of emergence.See the figure. The figure is as shown below:

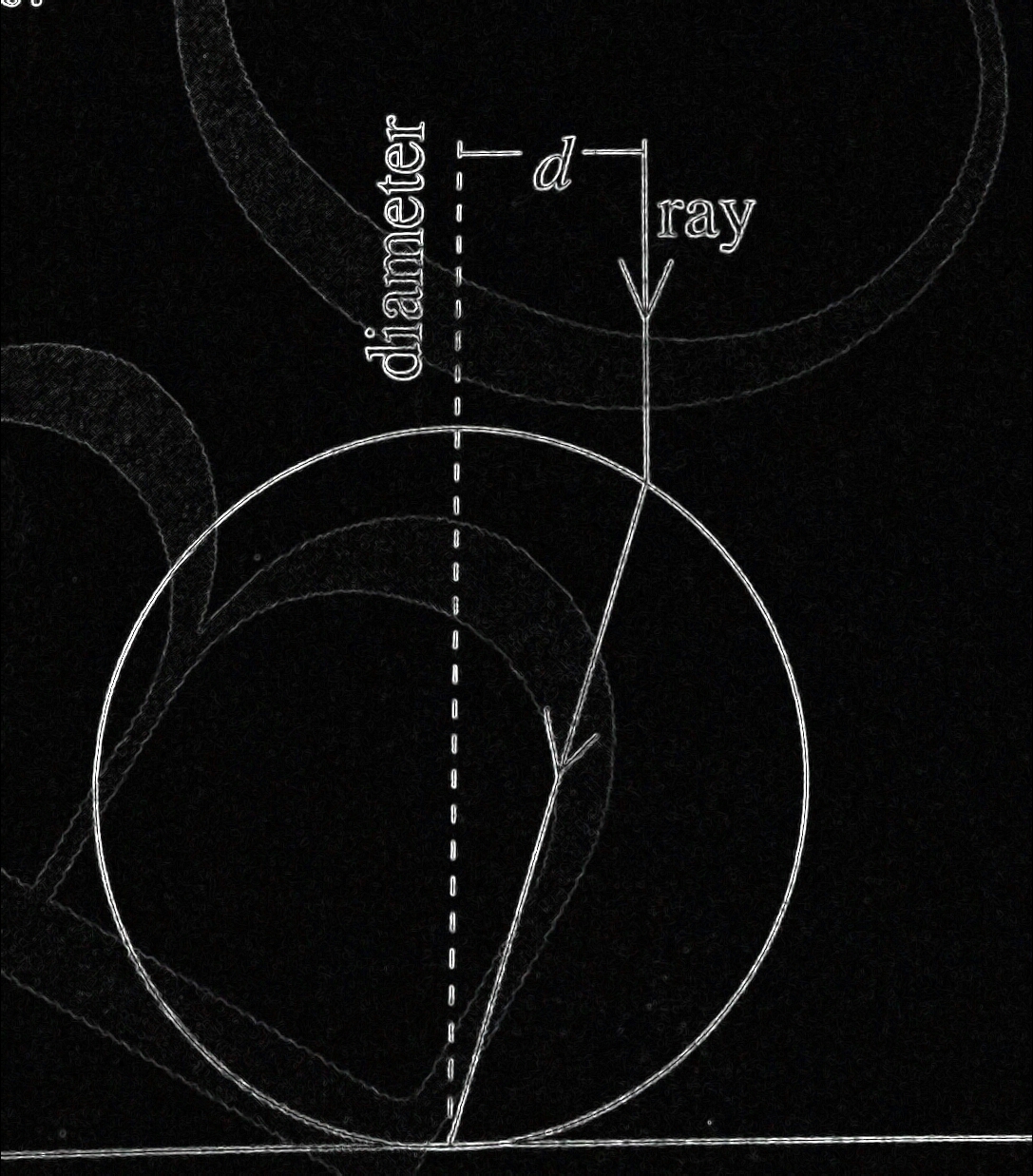
The answer is 3.414213562.

1 solution

Rajdeep Brahma
Jun 25, 2018

So we get $i=2r$

$\frac{sin(i)}{sin(r)}$ = $n$

$2cos(r)=n$

$sin(i)=$ $\frac{d}{r}$

$sin(2r)=$ $\frac{d}{r}$

Now using simple algebraic manipulation we get that $\frac{n^2}{2}$ = $\frac{r+\sqrt{r^2-d^2}}{r}$

$0<d<=r$

Hence $\sqrt{2}<n<=2$ .So the answer is $\sqrt{2}+2=3.414213562$

NOTE: THIS IS INPHO 2007 QUESTION SO NO CLAIM OF ORIGINALITY IS MADE

It's probably worth mentioning that d can't be zero.

Steven Chase - 2 years, 11 months ago

But, Sir isn't that obvious, because then, no refraction would take place........The light would pass undeviated.......

Aaghaz Mahajan - 2 years, 4 months ago

1 LAKH POINTS PROBLEM!!!!

The answer is 3.414213562.

1 solution

So we get i = 2 r i=2r i = 2 r

s i n ( i ) s i n ( r ) \frac{sin(i)}{sin(r)} s i n ( r ) s i n ( i ) ​ = n n n

2 c o s ( r ) = n 2cos(r)=n 2 c o s ( r ) = n

s i n ( i ) = sin(i)= s i n ( i ) = d r \frac{d}{r} r d ​

s i n ( 2 r ) = sin(2r)= s i n ( 2 r ) = d r \frac{d}{r} r d ​

Now using simple algebraic manipulation we get that n 2 2 \frac{n^2}{2} 2 n 2 ​ = r + r 2 − d 2 r \frac{r+\sqrt{r^2-d^2}}{r} r r + r 2 − d 2 ​ ​

0 < d < = r 0<d<=r 0 < d < = r

Hence 2 < n < = 2 \sqrt{2}<n<=2 2 ​ < n < = 2 .So the answer is 2 + 2 = 3.414213562 \sqrt{2}+2=3.414213562 2 ​ + 2 = 3 . 4 1 4 2 1 3 5 6 2

0 pending reports