1 move, big change

Let $b$ be the last digit of a number $10a+b$ . Then for some $x$

$10^x b + a=2(10a+b)$

which means that

$b=\dfrac{19a}{10^x-2}$

Since $b$ is a single digit, the smallest $x$ for which $10^x-2$ has $19$ as a factor is $x=17$ , so that the number is

$52631578947368420b+b$

Since $b=1$ leads to $52631578947368421$ , the double of which is $105263157894736842$ , we try the next value $b=2$ , which leads to

$105263157894736842$ , the double of which is $210526315789473684$

One solution for $n = 18$ is $x = 105263157894736842$ , since:

This $x$ value can be found with its last digit $2$ as a seed using the following algorithm. First, start with the seed $2$ and add it to itself to obtain $2 + 2 = 4$ .

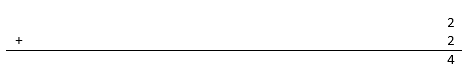
Then take the $4$ and place it in the next column and add it to itself to obtain $4 + 4 = 8$ .

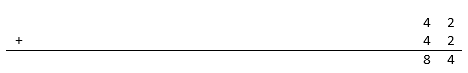
Then take the $8$ and place it in the next column and add it to itself to obtain $8 + 8 = 16$ . Put down the $6$ and carry the $1$ .

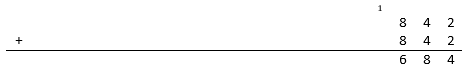
Then take the $6$ and place it in the next column and add it to itself (along with the carried $1$ ) to obtain $6 + 6 + 1 = 13$ . Put down the $3$ and carry the $1$ .

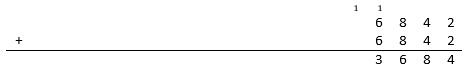
Continue this process until you obtain the original seed $2$ (without a carried $1$ ). The result, with $18$ digits, is the first image in this solution.

---

Now we can use this algorithm to test all $10$ digits and show that if it is possible they all result in solutions with $18$ digits:

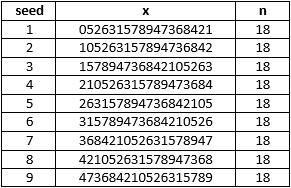
(Exceptions: The seed $0$ results in $x = 0$ , which does not have a last digit to move to the front, so it is discounted. Also, technically the seed $1$ results in an $x$ value with a leading $0$ , but the leading $0$ is necessary for the $2x$ value, so the number of digits is still $n = 18$ .)

Since all possible seeds result in solutions $x$ values with $18$ digits, the smallest possible $n$ value is $n = \boxed{18}$ .

---

Incidentally, all the possible solutions for $x$ have all the digits in the same order, and is an 18-digit cyclic number .