1- Numbering a Square
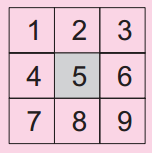 Paula has numbered all squares of the square board above, from left to right and top to bottom, starting with the number 1. The central square received the number 5. If she does the same with another square board divided by 49 squares, which number will be written on the central square?
Paula has numbered all squares of the square board above, from left to right and top to bottom, starting with the number 1. The central square received the number 5. If she does the same with another square board divided by 49 squares, which number will be written on the central square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Exactly like what I did
For 49 Square board ,this becomes a grid of 7X7..We take middle no of top row that is 4,so next column will be added 7 number and therefore the central square will be 4 +7+7+7 =25 Ans K.K.GARG,India
I like your approach .. impressive
BEST APPROACH
nice same approach
9/2 IS EQUAL TO 4.5 WHICH IS ROUNDED TO 5. SO JUST DIVIDE 49 (WHICH IS ALSO ODD) BY 2, WHICH WILL RESULT IN 24.5 ROUNDED TO EQUAL 25.
i also do the same process...... hehehe....
9 boxes + 1= 10/2 = 5, then 49+1=50/2 =25. that's it!
It's actually asking for the median, or the second quarter of a series, in which the formula for the position of the median is Q2= (n+1)/2. Since the data is ordered and and changes by one, we know that any position the data set is equal to its value. Since n=49 (49+1)/2=25 Meaning that 25 will be in the centre.
I thought this problem simply in terms of areas. A square can have areas of 1, 4,9,16,25....49 etc.. Since we have 49 squares, we can take the square root. Giving us 7 squares per row. Since its an odd number, we simply go to the middle row and column, which corresponds to 25.
9+1 =10, and then 10 divided by 2 equals five. 49+1=50, then 50 divided by 2 = 25
Notice also that the middle number is equal to the quotient of sum of one vertical, horizontal, or diagonal numbers of the square and the square root of total numbers of squares. (For 3x3 square: sum of each line = 15. square root of total number of squares = sqrt(9) = 3. 15/3 = 5) So for 7x7, 175/7 = 25.
In the given pattern of 3*3 matrix, position of middle term can be given as 3/2=1.5(round off to 2), i.e; middle term is on (2,2) position in the matrix. Now for the value of that middle term we have n^2+(n-1)^2 where, n=position of middle term
So, for the given pattern of 7*7 matrix position of middle term = 7/2= 3.5(round off to 4 ) hence, value of middle term = n^2+(n-1)^2 = 4^2 + (4-1)^2 = 25
It should be average of 1st and last number in every case.....it is as simple as that!!
If there's a 7 x 7 arrangement, the middlemost column would be the column containing 4. Now, looking row-wise, the middle most row will be the fourth one. Suppose the middlemost number is in the nth row. Then, we'll have to add 7*(n-1) to 4. Thus, we get the central number as 4 + 7(3) = 4 + 21 = 25.
since it is given as 49 so we will make a square of 7x7 and when we put the values in it we will notice that 25 comes in the middle.
nice one bro!
its 7^2 =49 .. the middle one will be 25 .. 5^2..
Makes no sense!!!
Add one to greater number and divide by two... ie. (n+1)/2
A square board with 49 squares has to be a 7x7 grid (7 squared).
The median (middle) number in 7 is the 4th number. The last number after three rows is 21 (7x3).
This means that the 4th number in the 4th row is 25.
Well, a unique central square will exist only if dimension is n x n , where n is odd and hence n^2 will be the total no. of squares or the last no. of the board. To find the central no., we can count all the squares till just before the middle row(i.e. (((n-1)/2) n) and then adding the middle element of the row(i.e. (n+1)/2).... Mathematically, central no.= (n-1) n/2+(n+1)/2 =(n^2+1)/2 or simply, = (Total no. of squares in the board+1)/2
So in this problem, as total no. of squares is 49, the central no. will be = (49+1)/2 =25 Ans.
Hope it helps
wow, what i do is just root the number of squares then use the centcr as coordinates
In the First Pattern, there were 9 boxes and the central number will be (9+1)/2=5.
For n boxes, the central Number will be (n+1)/2.
For 49 boxes, central no=(49+1)/2=25