10-seconds challenge-4

$e^{x}$ and $ln(x)$ are inverse of each other . Each one in mirror image of other about $y=x$ line

No intersection $\implies$ no solution

10 sec solution would be the graphical one.

The graphs of $\large e^x$ & $\large \ln(x)$ never intersect .

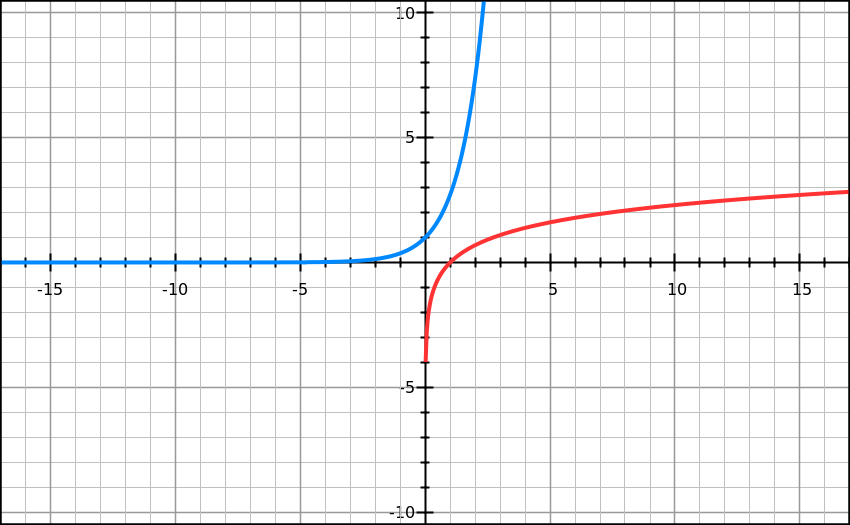I agree there are no real solutions, but there are two complex solutions, you should consider it in the problem. Nice problem

$e^x$ and $\ln(x)$ are inverse of each other and $e^x$ and $x$ don't intersect therefore there is no real solution.