10 Stones
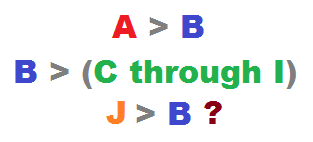
Ten stones all have distinct weights.
They are randomly labeled A through J.
The stone labeled B is weighed against all the other stones except J, and found to be heavier than all of them except A.
The probability that J is heavier than B is given as b a , where a and b are coprime positive integers.
What is a + b ?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
There are three possible orderings of the stones (heaviest to lightest):
- A B → rest
- A J B → rest
- J A B → rest
The number of ways of achieving each one is:
- A B → (rest): 8 !
- A J B → (rest): 7 !
- J A B → (rest): 7 !
So, the probability that J > B ( J is heavier than B ) is given by:
P = 7 ! + 7 ! + 8 ! 7 ! + 7 ! = 2 ⋅ 7 ! + 8 ⋅ 7 ! 2 ⋅ 7 ! = 1 0 2 = 5 1
1 + 5 = 6
This makes me think of another question ....
Suppose we are told instead that 8 of the stones have distinct weights and that 2 have the same weight, (distinct from the other 8 ), with all 4 5 possible "equal-pairings" being equally likely. If as before A > B and B is greater than C → I , what is the probability that J > B with this added condition? Is it less, the same, or greater than 1 / 5 ?
I think that the complication here is that there is an asymmetry in the possible equal-pairings left after the initial set of weighings. We have eliminated 1 5 of the 4 5 , ( A with 8 of the others and B with 7 of the others, (and with A as well but we've already counted that one)). 9 of the 30 pairings left can involve J , so there is a 1 / 3 0 chance of J being paired with A and the same of it being paired with B . There is then a 2 1 / 3 0 = 7 / 1 0 chance that J 's weight is distinct, in which case there are 9 positions in the weight order it can be placed in, (as in this case 2 of C → I are paired), leading to a 2 / 9 chance that it weighs more than B . The final probability that J > B is then
3 0 9 × 9 1 + 3 0 2 1 × 9 2 = 9 0 1 7 < 5 1 .
Does this sound reasonable? My concern is the 2 / 9 value; it might be 2 / 1 0 , but either way the final probability is less than 1 / 5 . This did make me think of another question, but I'll leave that for another time. :)
Log in to reply
Yeah, this is a much more interesting/involved problem... I must admit that when I wrote this problem I hadn't realized that I was just saying, "What is the probability that J is the heaviest or second heaviest?" which is trivially 1/5.
Lemme think about your question for a bit...
There's a lot of "noise" in this problem. To clear the noise, note that A , J > B > C through I just means " J is the heaviest or the second heaviest".
Out of 10 stones, what is the probability that we would choose either the heaviest or the second heaviest stone to be our "J"?
Answer: 1 0 2 = 5 1
so a + b = 1 + 5 = 6 .