Integral Solutions!
 A
=
{
1
,
2
,
3
,
5
,
6
,
1
0
,
1
5
,
3
0
}
A
=
{
1
,
2
,
3
,
5
,
6
,
1
0
,
1
5
,
3
0
}
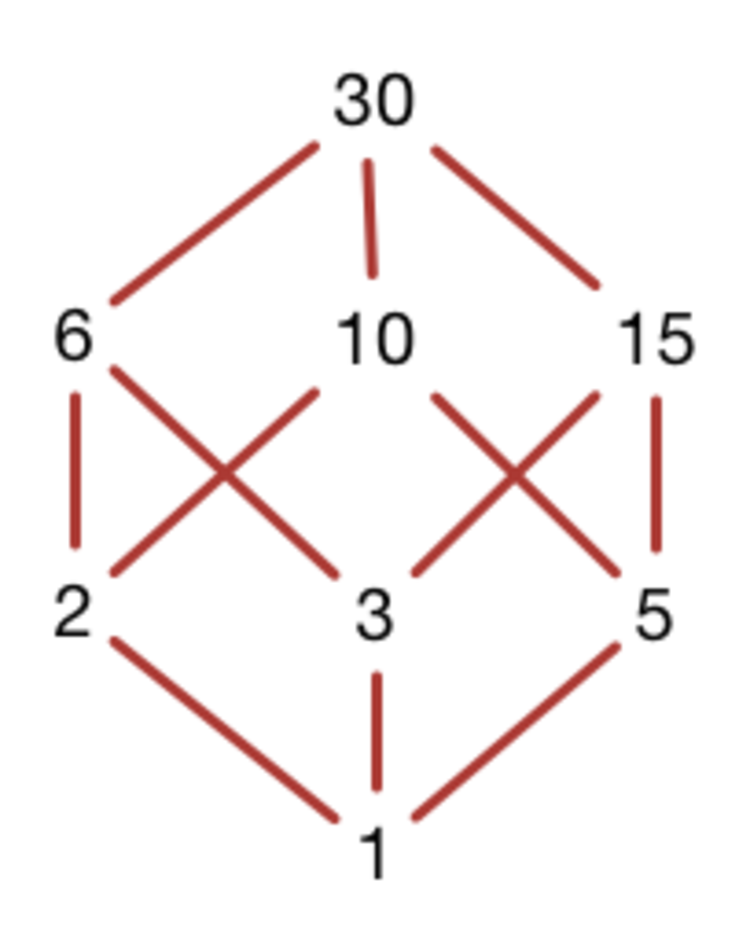
For set A , find the number of positive integral solution of ( x , y , z ) that satisfy the condition x y z ∈ a .
Too easy? Try this problem .
The answer is 64.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Yes, there is. This deserves to be a solution but I unfortunately lost my attempts:
Clearly, a is the set of divisors of 3 0 .
However, 3 0 = 2 × 3 × 5
Now, take three boxes: x , y , z
For each of 2 , 3 , 5 , you have four choices: To put it in x , to put it in y , to put it in z , to put it throw it away.
Thus, there are a total of 4 3 ways to do the things.
Log in to reply
ah nice, to put in same box is equivalent to forming their product, nice , i shall use this method from now on, thankyou :)
Yes , Same But I Reason it in slight different way : Let \xyzt = 2 ∗ 3 ∗ 5 where x,y,z are 3 Real beggars and 't' is false beggar , So you have 3 different books (2,3,5) which can be distributed in 4 3 ways where 1st Book (say 2) has 4 options 2nd Book (say 3) has 4 options 3rd Book (say 5) has 4 options
So total ways are = 4 ∗ 4 ∗ 4 And Thanks For Adding Link of Your Question , and also for Editing Now It looks Better ! ! ⌣ ¨
Great approach. We create this "fake variable" to help us solve questions like
Find the total number of ordered triples of non-negative integers such that a + b + c ≤ 1 0 0 .
is there a better way than to observe that all numbers must be powers of 2 and 5 and 3 and their products, from which 1 comes in one way , 2,3,5 in 3 ways each, 6,10,15 in 9 ways each(products of two taken at a time) and 30 in 27 ways (product of all 3) so total 64