100 Followers

Geometry Level 5

Let P = tan ⁡ θ 2 + 2 tan ⁡ θ + 4 tan ⁡ 2 θ + 8 cot ⁡ 4 θ P = \tan \dfrac \theta2 + 2\tan \theta + 4\tan2\theta + 8\cot4\theta and given that 1 1 − cos ⁡ θ + i sin ⁡ θ \dfrac1{1- \cos\theta + i \sin\theta} can be expressed in the form of a + b i a + bi , where a a and b b are real numbers with i = − 1 i = \sqrt{-1} . Compute a ⋅ b P \dfrac{a\cdot b}{ P } .


The answer is -0.25.

View wiki
Raj Rajput by RAJ RAJPUT , 25, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Raj Rajput
Jan 30, 2016

11 Helpful 0 Interesting 0 Brilliant 0 Confused

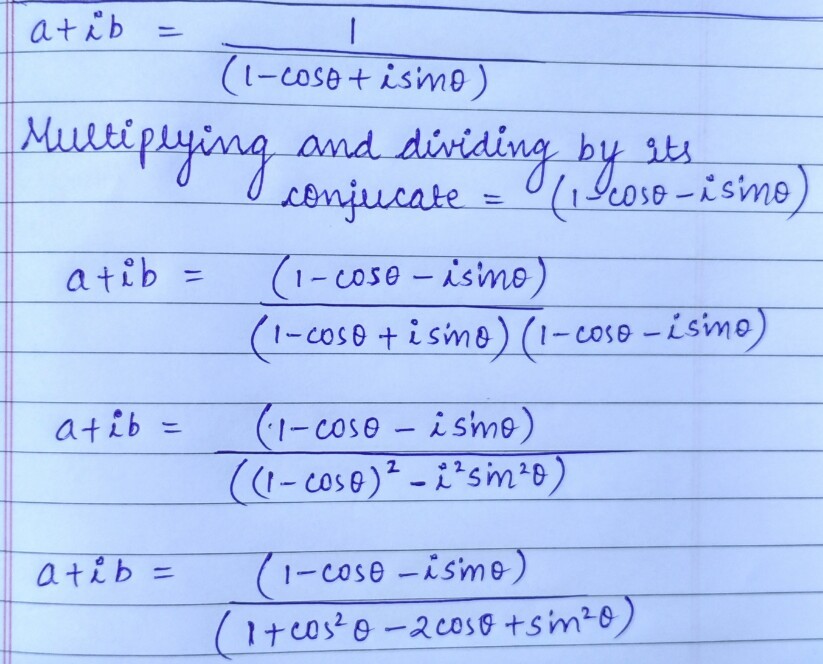
That is a wonderful answer,, but i m sorry because i don t understand the concept,, may you give more explanation about the concept,, thanks,,

Dea Driastuti - 5 years, 4 months ago

Log in to reply

Which point is difficult for you ??

RAJ RAJPUT - 5 years, 4 months ago
Ariel Gershon
Feb 4, 2016

Let x = tan ⁡ θ 2 x = \tan{\dfrac{\theta}{2}} . We can use the double-angle formula to get tan ⁡ ( θ ) = 2 x 1 − x 2 \tan{(\theta)} = \dfrac{2x}{1-x^2} . Applying the formula again and simplifying, we get: tan ⁡ ( 2 θ ) = 4 x ( 1 − x 2 ) 1 − 6 x 2 + x 4 \tan{(2\theta)} = \dfrac{4x(1-x^2)}{1-6x^2+x^4} . If we apply the formula one more time and take the reciprocal, we get: cot ⁡ ( 4 θ ) = 1 tan ⁡ ( 4 θ ) = ( 1 − 6 x 2 + x 4 ) 2 − 16 x 2 ( 1 − x 2 ) 2 8 x ( 1 − x 2 ) ( 1 − 6 x 4 + x 4 ) \cot{(4\theta)} = \dfrac{1}{\tan{(4\theta)}} = \dfrac{(1-6x^2+x^4)^2-16x^2(1-x^2)^2}{8x(1-x^2)(1-6x^4+x^4)}

Therefore, P = x + 4 x 1 − x 2 + 16 x ( 1 − x 2 ) 1 − 6 x 2 + x 4 + ( 1 − 6 x 2 + x 4 ) 2 − 16 x 2 ( 1 − x 2 ) 2 x ( 1 − x 2 ) ( 1 − 6 x 4 + x 4 ) P = x + \dfrac{4x}{1-x^2} + \dfrac{16x(1-x^2)}{1-6x^2+x^4} + \dfrac{(1-6x^2+x^4)^2-16x^2(1-x^2)^2}{x(1-x^2)(1-6x^4+x^4)} After some simplifying, the result is P = 1 x = cot ⁡ θ 2 P = \dfrac{1}{x} = \cot{\dfrac{\theta}{2}} .

Now onto the second part of the problem:

1 1 − cos ⁡ ( θ ) + i sin ⁡ ( θ ) = 1 − cos ⁡ ( θ ) − i sin ⁡ ( θ ) ( 1 − cos ⁡ ( θ ) ) 2 + sin ⁡ 2 ( θ ) = 1 − cos ⁡ ( θ ) − i sin ⁡ ( θ ) 2 − 2 cos ⁡ ( θ ) = 1 2 − sin ⁡ ( θ ) 2 − 2 cos ⁡ ( θ ) i \dfrac{1}{1-\cos(\theta)+ i \sin(\theta)} = \dfrac{1-\cos(\theta) - i \sin(\theta)}{(1-\cos(\theta))^2 + \sin^2(\theta)} = \dfrac{1-\cos(\theta) - i \sin(\theta)}{2 - 2\cos(\theta)} = \dfrac{1}{2} - \dfrac{\sin(\theta)}{2 - 2\cos(\theta)} i

Thus a = 1 2 a = \dfrac{1}{2} and b = − sin ⁡ ( θ ) 2 − 2 cos ⁡ ( θ ) b = - \dfrac{\sin(\theta)}{2 - 2\cos(\theta)} . Substitute sin ⁡ ( θ ) = 2 sin ⁡ θ 2 cos ⁡ θ 2 \sin(\theta) = 2\sin\dfrac{\theta}{2} \cos\dfrac{\theta}{2} and cos ⁡ ( θ ) = 1 − 2 sin ⁡ 2 θ 2 \cos(\theta) = 1 - 2\sin^2\dfrac{\theta}{2} :

b = − 2 sin ⁡ θ 2 cos ⁡ θ 2 4 sin ⁡ 2 θ 2 = − 1 2 cot ⁡ θ 2 b = - \dfrac{2\sin\dfrac{\theta}{2} \cos\dfrac{\theta}{2}}{4\sin^2\dfrac{\theta}{2}} = - \dfrac{1}{2}\cot\dfrac{\theta}{2}

Hence, a ∗ b P = 1 2 ∗ ( − 1 2 cot ⁡ θ 2 ) ÷ cot ⁡ θ 2 = − 1 4 \dfrac{a*b}{P} = \dfrac{1}{2} * \left(-\dfrac{1}{2}\cot\dfrac{\theta}{2}\right) ÷ \cot{\dfrac{\theta}{2}} = \boxed{\dfrac{-1}{4}}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Seriously you have done this or it was just to show another method regarding this problem ??

RAJ RAJPUT - 5 years, 4 months ago

Log in to reply

Yeah, this is how I actually solved it. Your method is a lot simpler but I didn't think of it.

Ariel Gershon - 5 years, 4 months ago

Log in to reply

Your method is a bit complicated but provides a positive thinking "STICKING TO BASICS FIRST" may even also solve the problem. Good work man :) :)

RAJ RAJPUT - 5 years, 4 months ago

Put theta =60° and get d ans

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Really........

Spandan Senapati - 4 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...