101 Followers Question by Dr. Warm

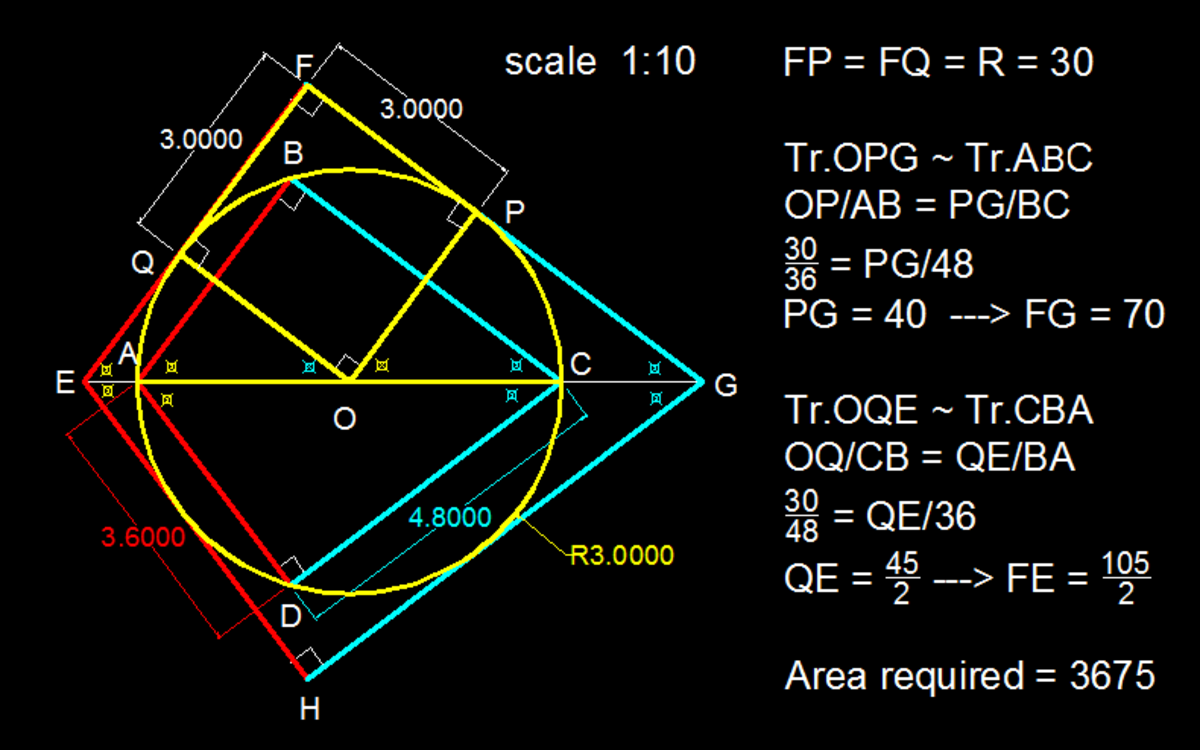
Geometrically, the kite can be inscribed in a circle if and only if it's the right kite, or the kite that has right angles. In other words, its long diagonal will be the diameter of the circumcircle.

Let $r$ be the radius of the circle in the question.

Then $4r^2 = 36^2 + 48^2$ .

$r = \sqrt{18^2 + 24^2} = 30$ .

Now considering the kite $EFGH$ , since all four sides are tangents of the circle, the radius $r$ will be the height of the the triangles with each side as the base.

Therefore, the area of $EFGH$ = $2\times(\dfrac{1}{2}\times r \times (EF+FG))$ .

Since both kites are similar, the ratio of the sides are the same. That is, $EF = k(AB) = 36k$ and $FG = k(BC) = 48k$ for some constant $k$ .

Thus, the area of $EFGH$ = $30\times (36k + 48k) = 2520k$ .

Alternatively, since the kite $EFGH$ is made up of two right triangles, the area also equals

$2\times(\frac{1}{2}\times EF \times FG)$ = $k^2(36\times 48$ ) = $1728k^2$ .

Solving for $k$ , we will get: $2520k = 1728k^2$ . $k = \dfrac{2520}{1728} = \dfrac{35}{24}$ .

Therefore, the area of $EFGH$ = $2520\times \dfrac{35}{24} = \boxed{3675}$ .

These are square kite. The radius of the circumcircle of small kite, $R=\frac 1 2 *\sqrt{36^2+48^2}=30.$
But this is the inradius of the big kite.
The right triangles are 3-4-5. If the kite has sides a, b, it area is ab, and inradius $\dfrac{ab}{a+b}=r.$
A square kite with side 3,4 will have inradius $r=\dfrac{3*4}{3+4}=\dfrac{12} 7. \ And\ the\ \ area = 3*4=12$
So the ratio between the sides of big kite and this 3,4 similar kite is $k=\dfrac{30}{\frac{12} 7 }=\frac{35}2.$
$Area\ of\ big\ kite=12*(\frac{35}2)^2= \Huge \color{#D61F06}{\ \ \ \ \ \ \ \ \ \ \ 3675.}$