115th Problem 2016

Electricity and Magnetism Level 1

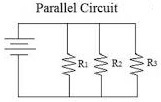
Given the parallel circuit above with the following values:

R 1 = 100 Ω R 2 = 300 Ω R 3 = 600 Ω V T = 150 V { R }_{ 1 }=100\Omega \\ \\ { R }_{ 2 }=300\Omega \\ \\ { R }_{ 3 }=600\Omega \\ \\ { V }_{ T }=150V

Find the I 2 { I }_{ 2 } or (current of R 2 { R }_{ 2 } ) of the circuit.

Part One .

Check out the set: 2016 Problems .

This is part three of the problem.


The answer is 0.5.

Angela Fajardo by Angela Fajardo , 19, Philippines

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Viki Zeta
Jul 15, 2016

Resistance = 300 Ω \Omega

Therefore

V = I R ⟹ I = V R ⟹ I = 150 300 = 0.5 V = IR \\ \implies I = \frac{V}{R} \\ \implies I = \frac{150}{300} = \fbox{0.5}

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Ashish Menon
Jul 15, 2016

Voltage in a parallel circuit is constant and the current across each resistance is given by V T R \dfrac{V_T}{R} .
So, I 2 = V T R 2 = 150 300 = 0.5 A I_2 = \dfrac{V_T}{R_2}\\ \\ = \dfrac{150}{300}\\ \\ = \color{#3D99F6}{\boxed{0.5 A}} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...