1:2
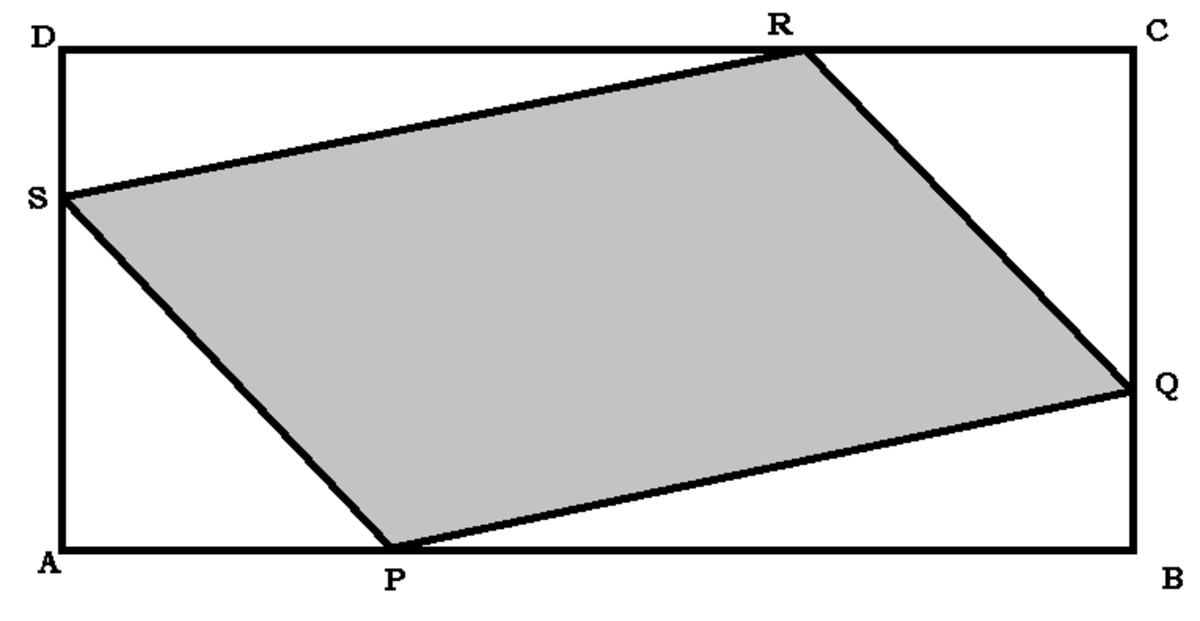
Points P , Q , R and S divide the respective sides of rectangle A B C D in the proportion 1 : 2 . If the area of rectangle A B C D is 1 , find the area quadrilateral P Q R S .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
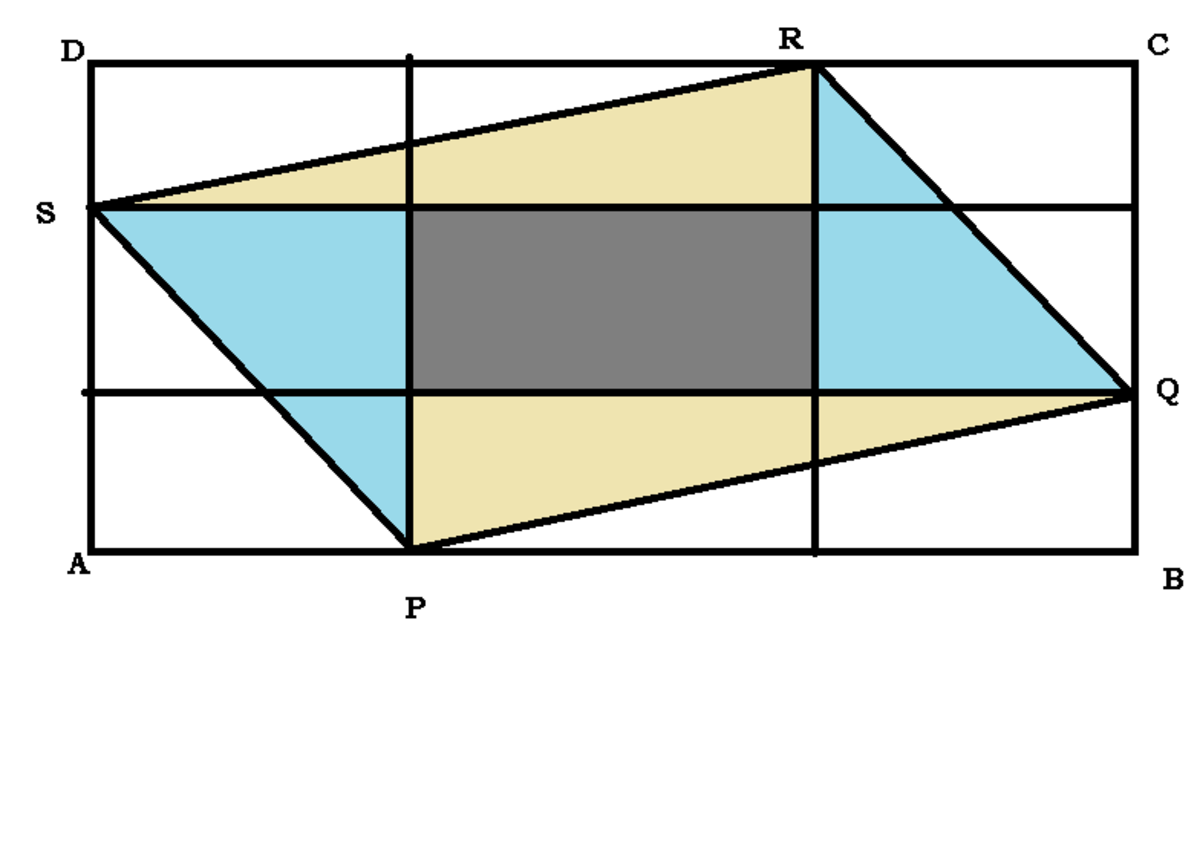 As we can see, we can divide the side in the proportion 1:1:1, and it will look like this. There are 4 triangles, that are the half of the rectangle where they are. And there's also a rectangle in the middle, whose area is
3
1
l
×
3
1
l
=
9
1
A
A
B
C
D
And the triangles are the other
9
8
, so it's
2
1
×
9
8
+
9
1
=
9
5
As we can see, we can divide the side in the proportion 1:1:1, and it will look like this. There are 4 triangles, that are the half of the rectangle where they are. And there's also a rectangle in the middle, whose area is
3
1
l
×
3
1
l
=
9
1
A
A
B
C
D
And the triangles are the other
9
8
, so it's
2
1
×
9
8
+
9
1
=
9
5
Very nice solution!
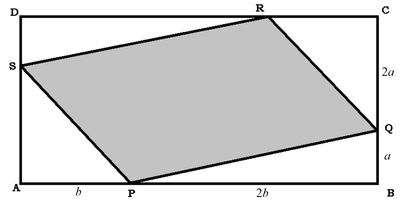
Let the height and breadth of rectangle A B C D be 3 a and 3 b respectively. Then the area of quadrilateral P Q S R is:
[ P Q R S ] ⟹ [ A B C D ] [ P Q R S ] = [ A B C D ] − [ A P S ] − [ B P Q ] − [ C Q R ] − [ D R S ] = ( 3 a ) ( 3 b ) − 2 1 ( 2 a ) b − 2 1 a ( 2 b ) − 2 1 ( 2 a ) b − 2 1 a ( 2 b ) = 9 a b − a b − a b − a b − a b = 5 a b = 9 5