12 circles
We have triangle
A
B
C
witn
O
- circumceter. We have 12 circles tangent the lines
A
B
,
A
C
,
C
B
,
A
O
,
B
O
,
C
O
- 6 circles are inside triangle
A
B
C
with radius
r
1
,
r
2
,
r
3
,
r
4
,
r
5
,
r
6
and 6 circles are outside triangle
A
B
C
with radius
R
1
,
R
2
,
R
3
,
R
4
,
R
5
,
R
6
.
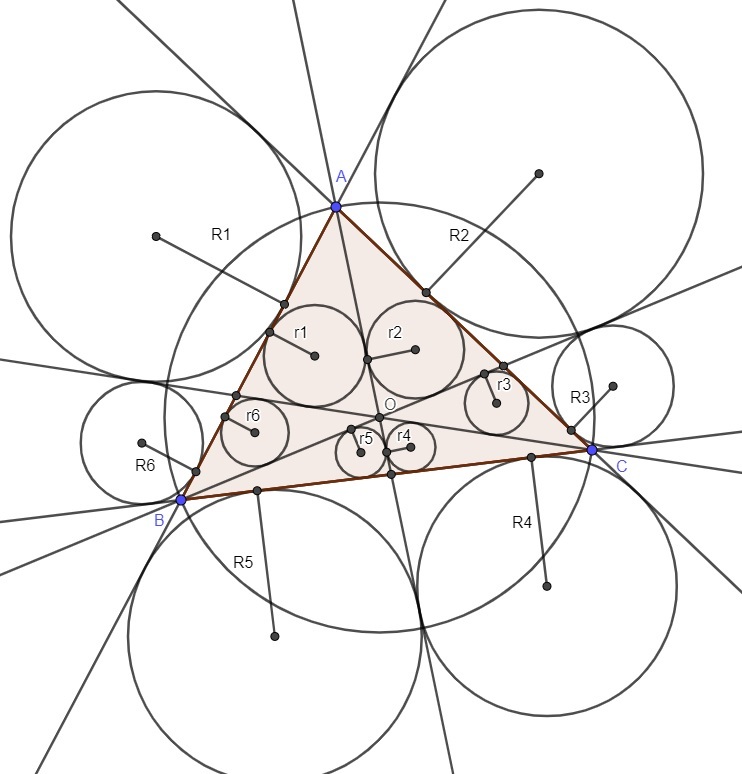
Proof 1 . r 1 1 + r 3 1 + r 5 1 = r 2 1 + r 4 1 + r 6 1 2 . R 1 1 + R 3 1 + R 5 1 = R 2 1 + R 4 1 + R 6 1
Find value A
A = R 1 1 + R 3 1 + R 5 1 r 1 1 + r 3 1 + r 5 1
Firth part problem give Stanley Rabinowitz for internal circles here .
Update. David Vreken send the message that this problem is not correct. And problem to reform. Find the value of the integer part of A .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The shortcut for this question is to start with an equilateral triangle and calculate r 1 = r 3 = r 5 = 4 3 − 1 r (for r = A O ) and R 1 = R 3 = R 5 = 4 3 3 − 1 r . Then that would mean R 1 1 + R 3 1 + R 5 1 r 1 1 + r 3 1 + r 5 1 = 3 .
For a more general solution for other triangles, let A ′ be the intersection of A O and B C , B ′ be the intersection of B O and A C , and C ′ be the intersection of C O and A B . Let r = A O = B O = C O .
Since an inscribed angle is half of a central angle that subtends the same arc, ∠ B O C = 2 A , so ∠ B O C ′ = ∠ C O B ′ = 1 8 0 ° − 2 A (from the straight line), ∠ C B O = ∠ B C O = 9 0 ° − A (from the isosceles triangle △ B O C ), and B C = 2 r sin A (from a circle chord). Similarly, ∠ A O C ′ = ∠ C O A ′ = 1 8 0 ° − 2 B and ∠ A O B ′ = ∠ B O A ′ = 1 8 0 ° − 2 C , ∠ A C O = ∠ C A O = 9 0 ° − B and ∠ A B O = ∠ B A O = 9 0 ° − C , and A B = 2 r sin C and A C = 2 r sin B .
Using the law of sines on △ B O A ′ gives O A ′ = cos ( B − C ) r cos A and B A ′ = cos ( B − C ) r sin 2 C . Similarly, O B ′ = cos ( A − C ) r cos B and O C ′ = cos ( A − B ) r cos C , and C A ′ = cos ( B − C ) r sin 2 B , C B ′ = cos ( A − C ) r sin 2 A , A B ′ = cos ( A − C ) r sin 2 C , A C ′ = cos ( A − B ) r sin 2 B , and B C ′ = cos ( A − B ) r sin 2 A .
Since the radius r of an incircle is the quotient of the area of its triangle and the semiperimeter of its triangle, r 1 = 2 1 ( r + cos ( A − B ) r sin 2 B + cos ( A − B ) r cos C ) 2 1 ⋅ r ⋅ cos ( A − B ) r sin 2 B ⋅ sin ( 9 0 ° − C ) = cos A sin A + cos A cos B r cos A cos B cos C .
Similarly:
r 3 = cos C sin C + cos C cos A r cos A cos B cos C
r 5 = cos B sin B + cos B cos C r cos A cos B cos C
r 2 = cos A sin A + cos A cos C r cos A cos B cos C
r 4 = cos C sin C + cos C cos B r cos A cos B cos C
r 6 = cos B sin B + cos B cos A r cos A cos B cos C
Therefore,
r 1 1 + r 3 1 + r 5 1 = r 2 1 + r 4 1 + r 6 1 = r cos A cos B cos C cos A sin A + cos B sin B + cos C sin C + cos A cos B + cos B cos C + cos A cos C
Since the radius R of an excircle is the quotient of the area of its triangle and the difference of the semiperimeter of its triangle and the side it is tangent to, R 1 = 2 1 ( 2 r sin B + r + cos ( A − B ) r cos C + cos ( A − B ) r sin 2 B ) − cos ( A − B ) r sin 2 B 2 1 ⋅ 2 r sin B ⋅ ( r + cos ( A − B ) r cos C ) ⋅ sin ( 9 0 ° − B ) = 2 sin A sin B sin C cos A cos B + sin A sin B cos A cos B − sin B cos A cos B cos C − sin B cos A cos 2 B 2 r sin A sin B sin C cos A cos B cos C .
Similarly:
R 3 = 2 sin A sin B sin C cos A cos C + sin A sin C cos A cos C − sin A cos A cos B cos C − sin A cos C cos 2 A 2 r sin A sin B sin C cos A cos B cos C
R 5 = 2 sin A sin B sin C cos B cos C + sin B sin C cos B cos C − sin C cos A cos B cos C − sin C cos B cos 2 C 2 r sin A sin B sin C cos A cos B cos C
R 2 = 2 sin A sin B sin C cos A cos C + sin A sin C cos A cos C − sin C cos A cos B cos C − sin C cos A cos 2 C 2 r sin A sin B sin C cos A cos B cos C
R 4 = 2 sin A sin B sin C cos B cos C + sin B sin C cos B cos C − sin B cos A cos B cos C − sin B cos C cos 2 B 2 r sin A sin B sin C cos A cos B cos C
R 6 = 2 sin A sin B sin C cos A cos B + sin A sin B cos A cos B − sin A cos A cos B cos C − sin A cos B cos 2 A 2 r sin A sin B sin C cos A cos B cos C
Careful examination shows that:
R 1 1 + R 3 1 + R 5 1 = R 2 1 + R 4 1 + R 6 1
only for acute isosceles (and equilateral) triangles, but not for scalene triangles.
Finally, using the above equations, R 1 1 + R 3 1 + R 5 1 r 1 1 + r 3 1 + r 5 1 = 3 for equilateral triangles, but R 1 1 + R 3 1 + R 5 1 r 1 1 + r 3 1 + r 5 1 > 3 for all other acute triangles. In either case, the value of the integer part is 3 .