Twelve Points On Two Orbits

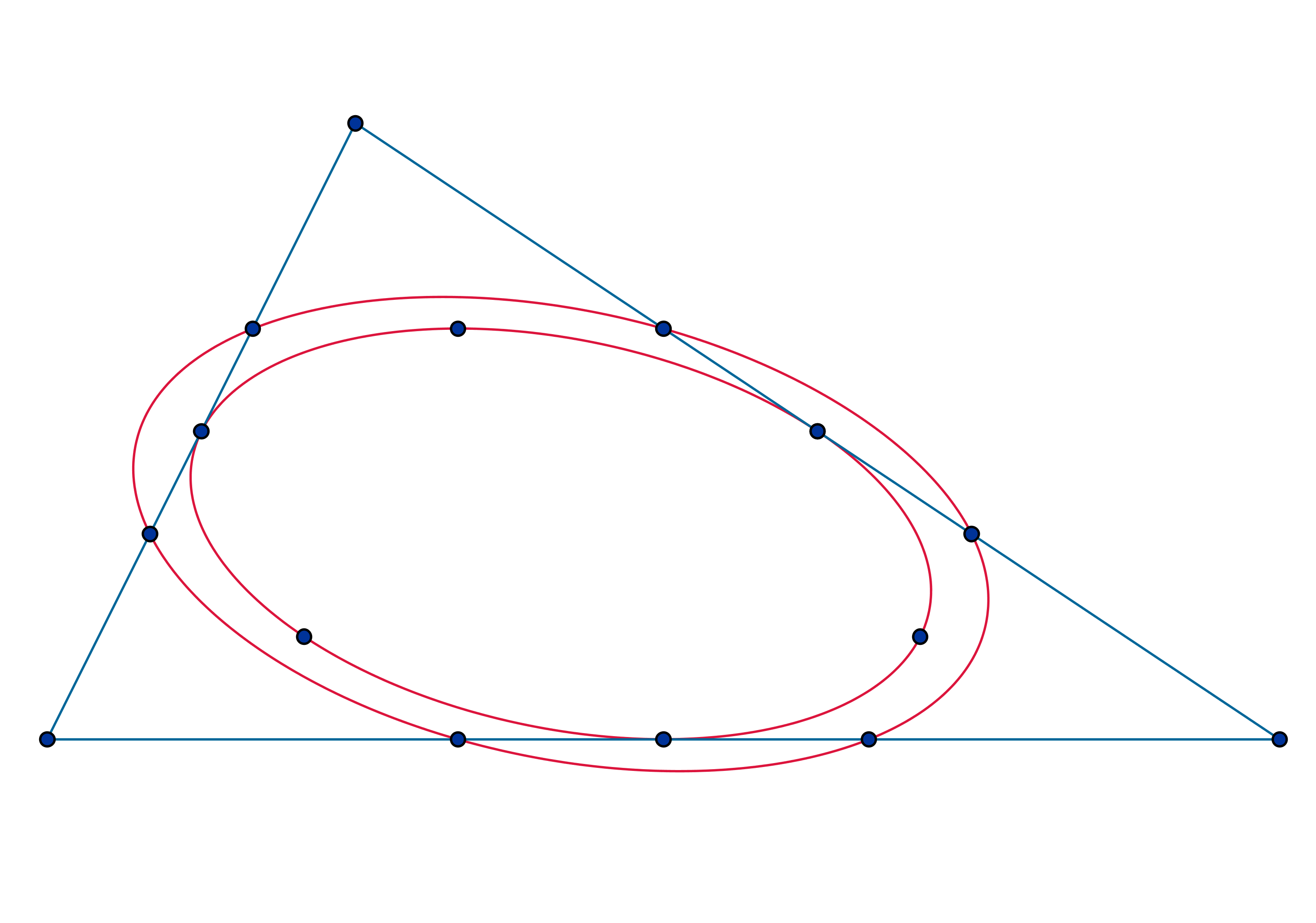
A triangle has vertices $A=(0,0), B=(24,0), C=(6,12)$ . The equation of its Steiner inellipse has the form: $a{ y }^{ 2 }+bxy+{ cx }^{ 2 }+dy+ex+f=0$

where $a, b, c, d, e, f$ are co-prime integers with $a>0$ .

The equation of another ellipse that trisects all three sides of triangle $ABC$ has the equation:

$a{ y }^{ 2 }+bxy+{ cx }^{ 2 }+dy+ex+f_2=0$

where $a, b, c, d, e, f_2$ are co-prime integers, and $a>0$ .

If $\dfrac{f}{f_2}=\dfrac{m}{n}$ , where $m,n$ are coprime positive integers, find $m + n.$

---

The problem is original