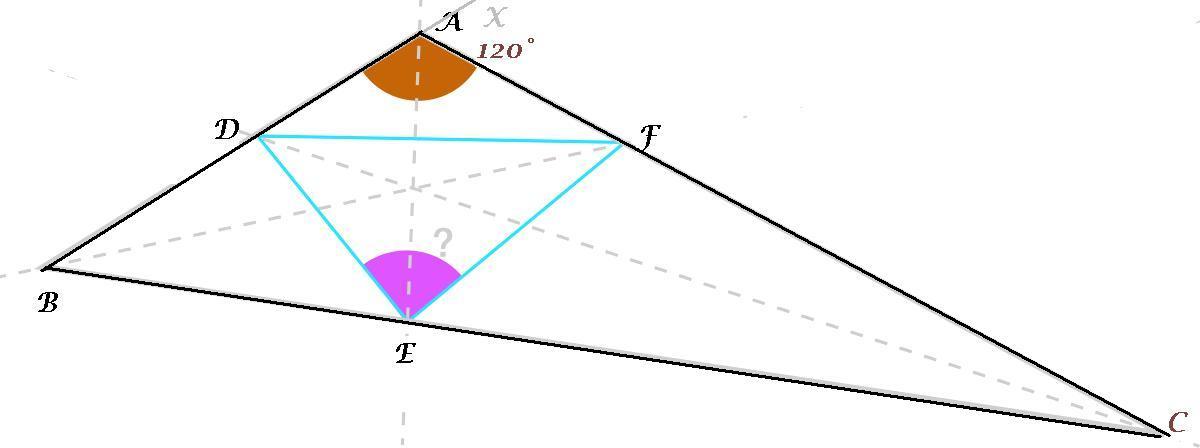
120 angle
Let be a triangle with . Suppose that the bisectors of angles and meet sides and at points and , respectively.
Find the measure of the largest angle of triangle (in degrees).
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Use the nomenclature as shown. Extend BA to say 'X'. <XAC=60° since <BAC=120° and this implies that AC bisects <XAE Now consider the triangle ABE in which we have one internal angle bisector and one external angle bisector intersecting in point F. Hence we conclude that EF bisects the <AEC externally. Likewise, ED bisects <AEB externally. Since, ED & EF are bisectors of <AEB & <AEC respectively, ED is perpendicular to EF or <DEF=90°.