The coloring... again

Suppose that the origin lies at the triangle vertex that is one of the three vertices of the yellow triangle, and let the other two triangle vertices have position vectors $\mathbf{a}$ and $\mathbf{b}$ with respect to the origin. If the endpoints of the line that defines the yellow triangle have position vectors $\lambda\mathbf{a}$ and $\mu\mathbf{b}$ for some $0 < \lambda,\mu < 1$ , then the yellow triangle has area $\tfrac12\lambda\mu|\mathbf{a}\times\mathbf{b}|$ , while the whole triangle has area $\tfrac12|\mathbf{a}\times\mathbf{b}|$ . Thus the ratio of the yellow and green areas is $\frac{\lambda\mu}{1-\lambda\mu}$ .

The centroid of the triangle has position vector $\tfrac13(\mathbf{a}+\mathbf{b})$ , and the three points with position vectors $\lambda\mathbf{a}$ , $\tfrac13(\mathbf{a}+\mathbf{b})$ and $\mu\mathbf{b}$ must be collinear, which implies that $\mu = \frac{\lambda}{3\lambda - 1}$ . For this to be consistent with the fact that both $\lambda$ and $\mu$ lie between $0$ and $1$ , we deduce that in fact $\tfrac12 < \lambda,\mu < 1$ .

Thus we need to minimize $\frac{\lambda\mu}{1 - \lambda\mu} = \frac{\lambda^2}{3\lambda - 1 - \lambda^2}$ over the range $\tfrac12 < \lambda < 1$ . This happens when $\lambda = \mu = \tfrac23$ . The minimum ratio is $\boxed{\tfrac45}$ .

If the line division is not parallel to the third side, then the yellow section below the parallel and the green section above the parallel can be switched by a 180° rotation (as pictured below), giving a yellow area larger than a yellow area of a parallel line division.
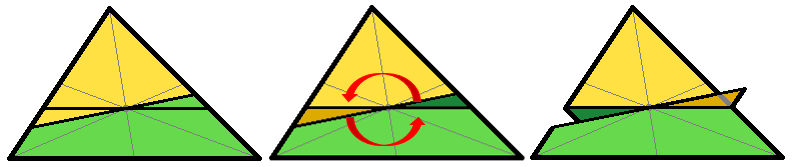Therefore, a minimum yellow area (and a minimum yellow to green ratio) must occur when the line through the centroid is parallel to the third side of the triangle.

Since all centroids divide a median in a 2:1 proportion, a second parallel line can be drawn through the yellow section halfway up, and 1 of its 2 parts would be equal to 1 of the 4 parts along the parallel line through the centroid, and 1 of the 6 parts along the base. The triangle can then be subdivided into congruent parallelograms using the base and the median though the base as guidelines (as pictured below), and the each of triangular parts can be matched with a matching triangular part through a 180° rotation to form more congruent parallelograms (also pictured below). 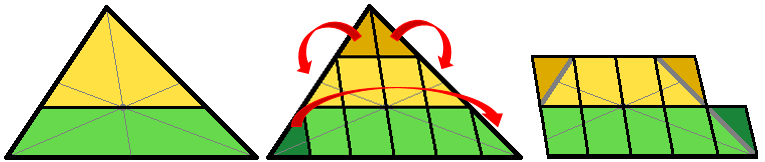After all the transformations, there are 9 congruent parallelograms – 4 yellow and 5 green, for a ratio of 4/5 or 0.8.

This is a brute force method using calculus. Assume we have a right triangle $ABC$ with coordinates $A(0,0)$ , $B(0,3)$ , and $C(3,0)$ . This way, the centroid is at point $1,1$ . Now, assume our line has y intercept $\alpha$ and crosses through the centroid to make a triangle with the x and y axis. The equation for the line would then be $y=(1-\alpha)x+\alpha$ . To find the x intercept, we set $y=0$ to get $x=\frac{\alpha}{\alpha -1}$ . Then the formula for the triangle, which we'll generalize to a rectangle, would be $A=\alpha\cdot\frac{\alpha}{\alpha -1}$ . Then the ratio of the yellow triangle to the quadrilateral would then be $\frac{A}{3\cdot3 - A}$ . We can now take the derivative and solve for $\alpha$ , giving us our answer. $\begin{aligned}&\frac{d}{d\alpha}\frac{\frac{\alpha^2}{\alpha -1}}{9-\frac{\alpha^2}{\alpha -1}}= \frac{d}{d\alpha}\frac{\frac{\alpha^2}{\alpha -1}}{\frac{9\alpha-9-\alpha^2}{\alpha -1}}=\frac{d}{d\alpha}\frac{\alpha^2}{9\alpha-9-\alpha^2}\\ &\frac{18\alpha^2-18\alpha-2\alpha^3-9\alpha^2+2\alpha^3}{(9\alpha-9-\alpha^2)^2} = \frac{9\alpha^2-18\alpha}{(9\alpha-9-\alpha^2)^2}=0 \\ &9\alpha^2-18\alpha=0 \implies \alpha=2 \end{aligned}$ Putting this back in the ratio function, we get $\frac{2^2}{9(2)-9-2^2}=\boxed{\frac{4}{5}}$

Looking at the first two samples, the ratios won't be changed if the top point is moved. So the triangle may as well be equilateral. As the line slants left or right towards a corner, the ratio approaches 1. So the ratio is minimized when the line is horizontal.

The centroid is 1/3 of the way up. So the horizontal line makes a yellow triangle 2/3 of size, or 4/9 the area of the whole triangle. So the quadrilateral is the other 5/9. The ratio between them is 4/5 = 0.8

PFA the solution!