15 points
Each of an equilateral triangle's sides is divided into five equal parts.
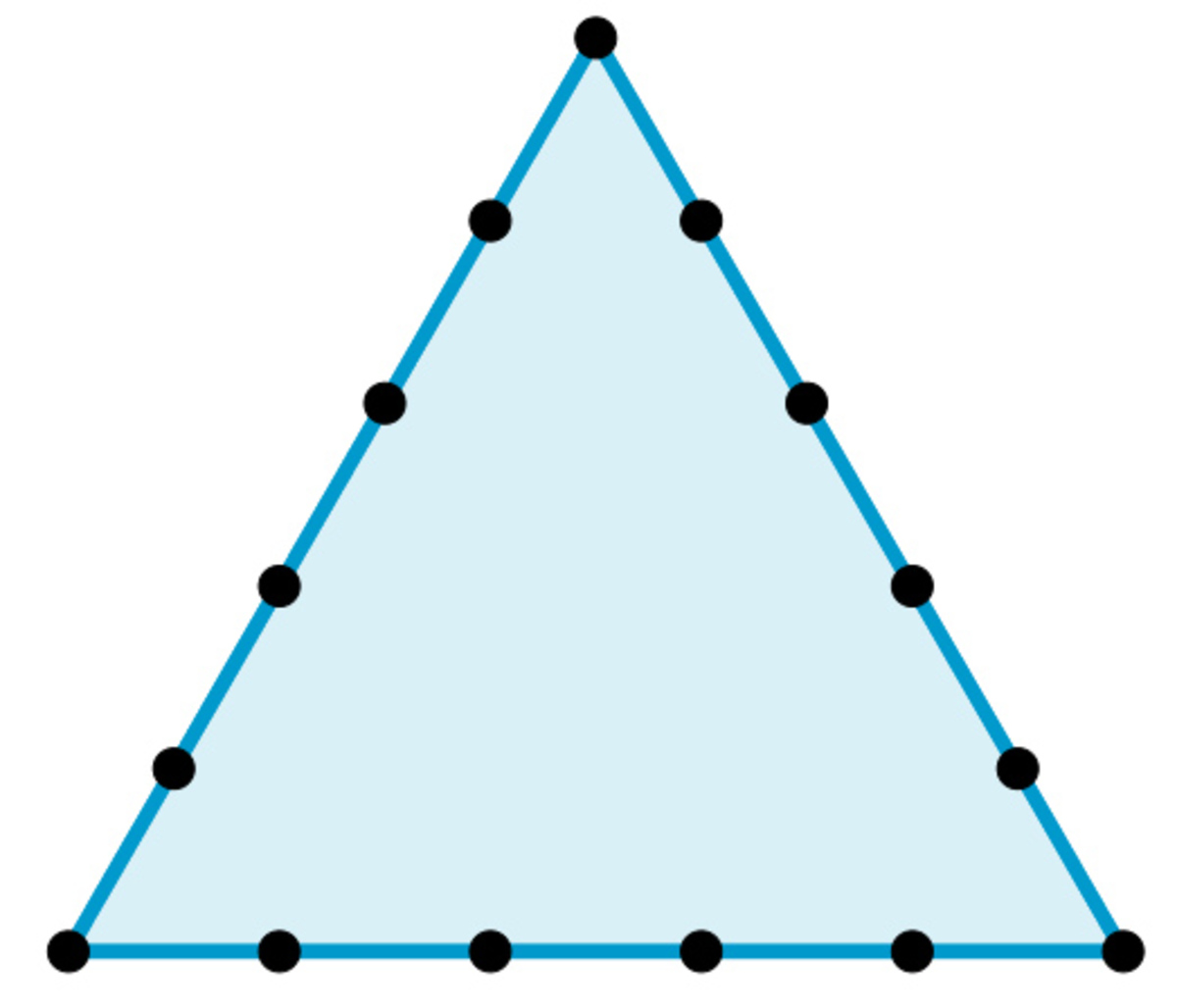
How many triangles are there, such that all of their vertices are from the 15 points?
The answer is 395.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If we want to choose three points, we can do it ( 3 1 5 ) = 1 ∗ 2 ∗ 3 1 5 ∗ 1 4 ∗ 1 3 = 4 5 5 ways. The three points always define a triangle, except they are on the same line. There are three lines, and there are 6 points in each of them. Since three points can't be on two lines at the same moment, from the 4 5 5 ways 3 ∗ ( 3 6 ) = 3 ∗ 1 ∗ 2 ∗ 3 6 ∗ 5 ∗ 4 = 6 0 ways aren't make solutions.
Therefore the answer is 4 5 5 − 6 0 = 3 9 5 .