150 Friends Problem

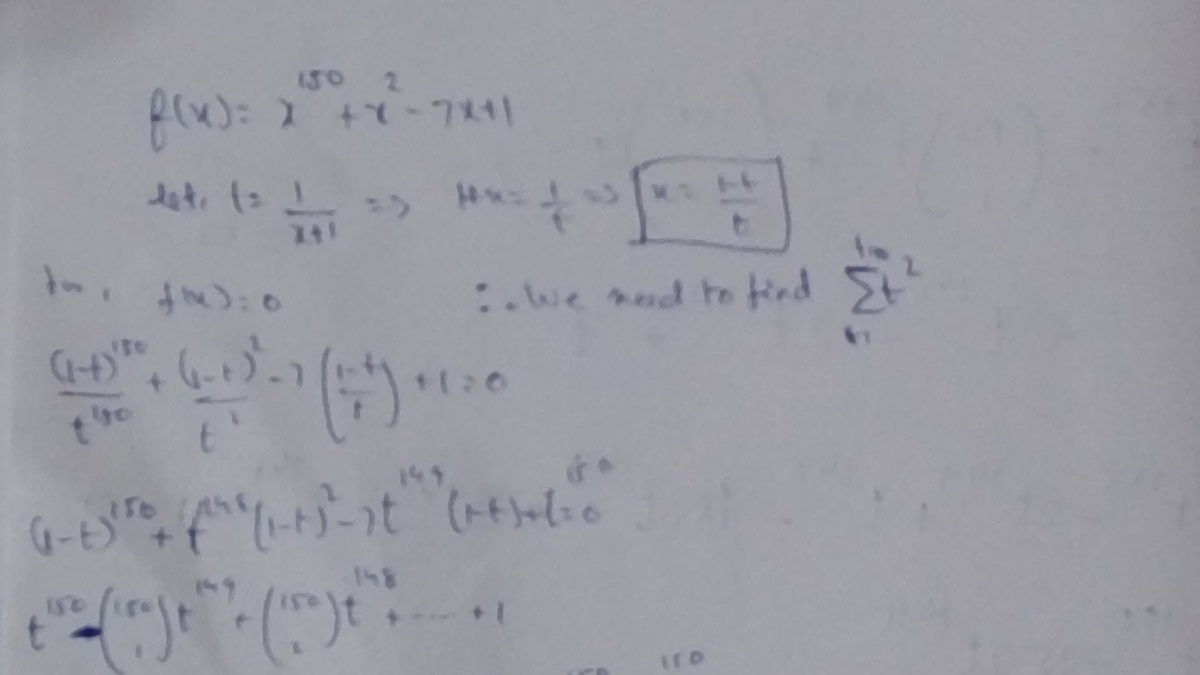
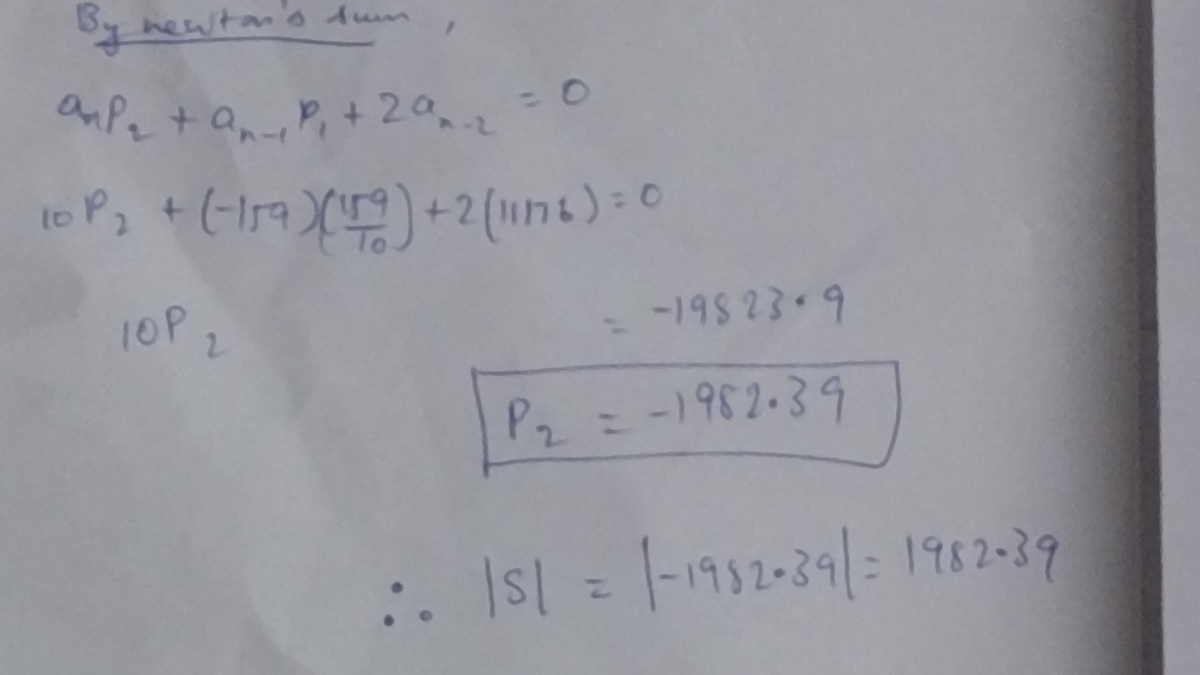
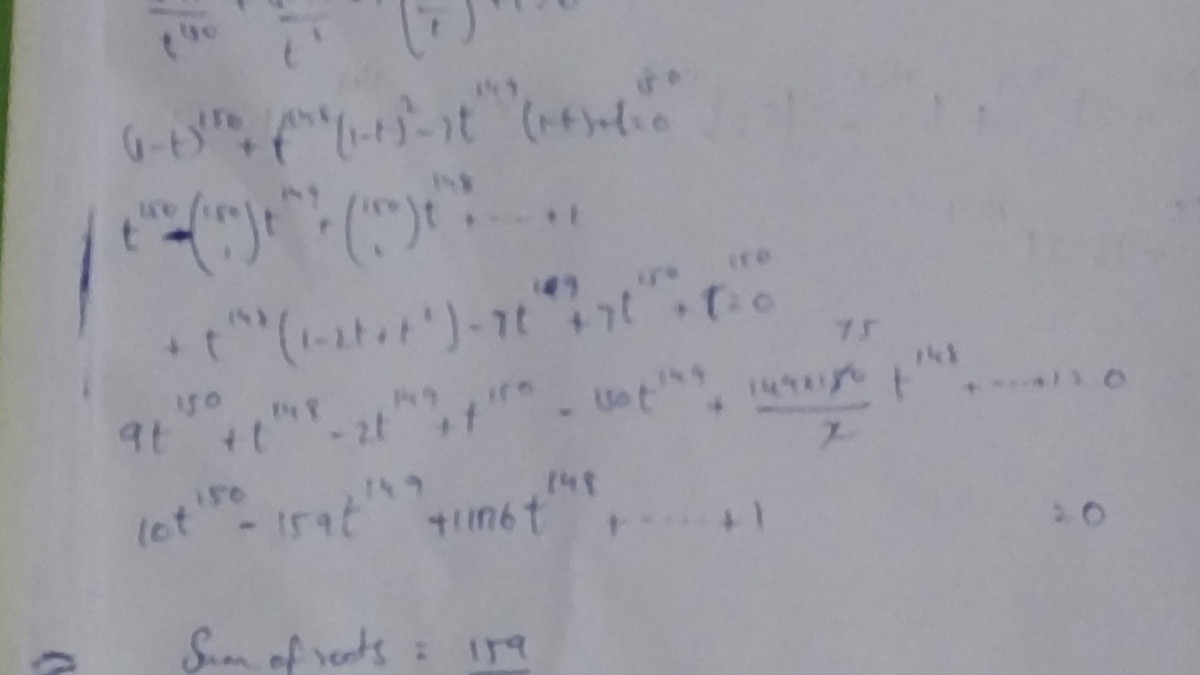
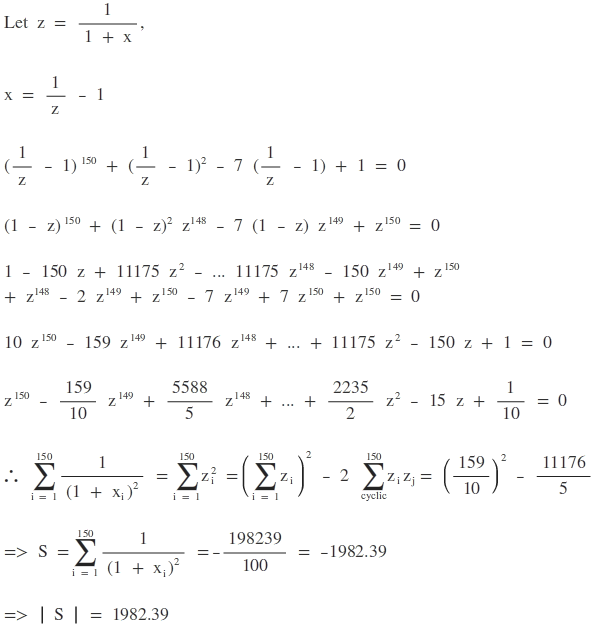
Since, $x_{1}, x_{2}, \ldots x_{150}$ are the roots of $f(x)$ .

So, $f(x) = (x-x_{1})(x-x_{2}) \ldots (x-x_{150})$ .

Differentiating it w.r.t $x$ and dividing it with $f(x)$ . We get

$\dfrac{f'(x)}{f(x)} = \sum_{i=1}^{150} \dfrac{1}{x-x_{i}}$

Differentiating again w.r.t $x$ . We get,

$\dfrac{(f'(x))^{2} - f(x)f''(x)}{f^2 (x)} = - \sum_{i=1}^{150}\dfrac{1}{\left(x -x_{i}\right)^{2}}$

Taking $x = -1$ , we get, $\dfrac{(f'(-1))^{2} - f(-1)f''(-1)}{f^2 (-1)} = - \sum_{i=1}^{150}\dfrac{1}{\left(-1 -x_{i}\right)^{2}}$

But we have $f(-1) = 10$ , $f'(-1) = -159$ and $f''(-1) = 22352$ . Substituting and solving them we get,

$S = \sum_{i=1}^{150}\dfrac{1}{\left(1 +x_{i}\right)^{2}} = -1982.39$

So, $|S| = \boxed{1982.39}$ .

let t=1/1+x =>x=(1-t)/t sub x=(1-t)/t in f(x)=o we get, (1-t)^{150}+t^{148}*(1-t)^{2}-7t^{149}(1-t)+t^{150}=0 we get binomial expansion given the pic.