16 Sides
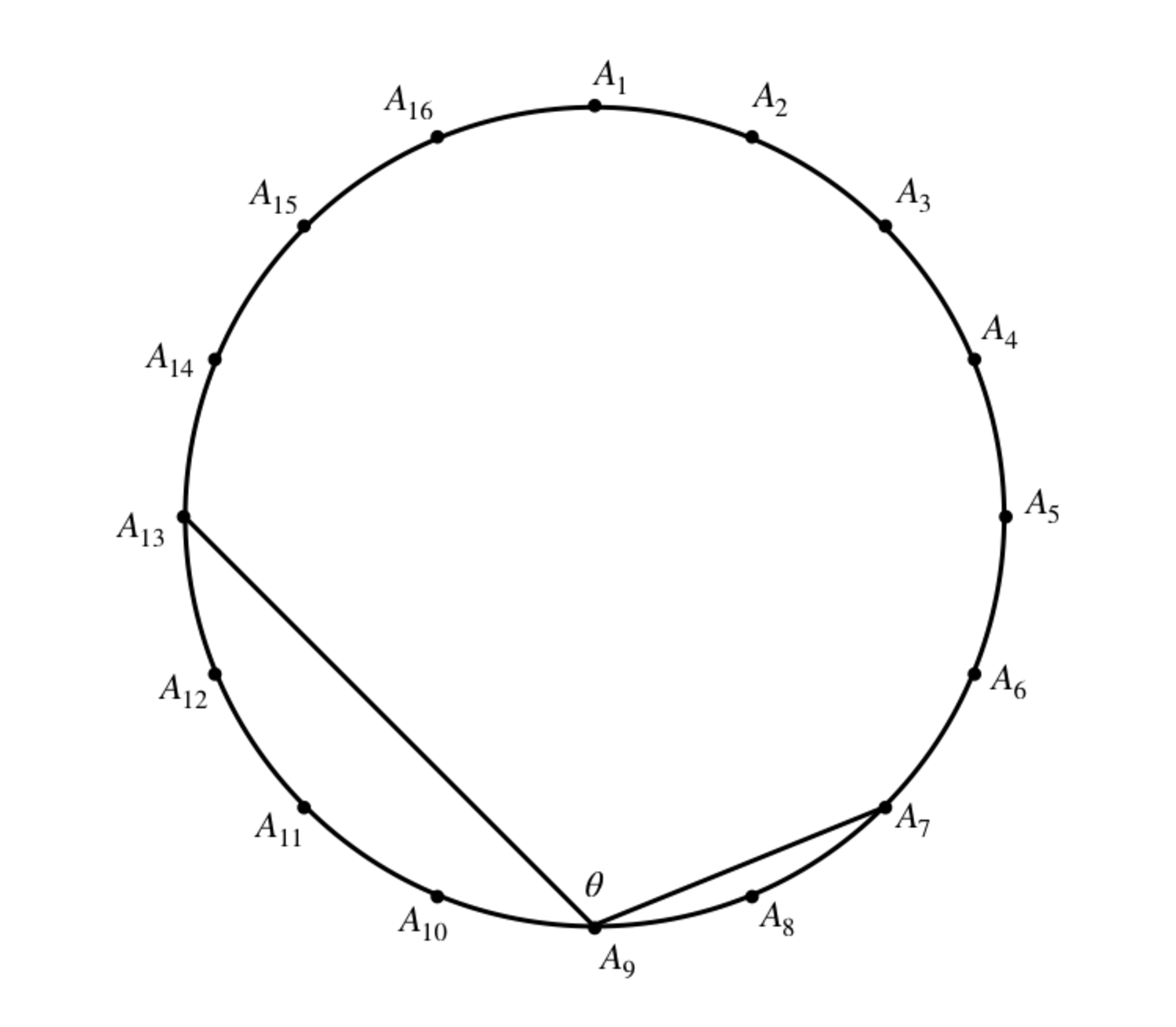
On a circle sixteen points, A 1 , A 2 , A 3 , ... A 1 6 , are equally spaced. What is the measure of ∠ A 7 A 9 A 1 3 in degrees?
The answer is 112.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
That's brilliant, I was thinking of cyclic quadrilaterals in solution but could not create any such concrete equations. Great :)
Let O be the center of the circle and draw A 1 3 O and A 7 O .
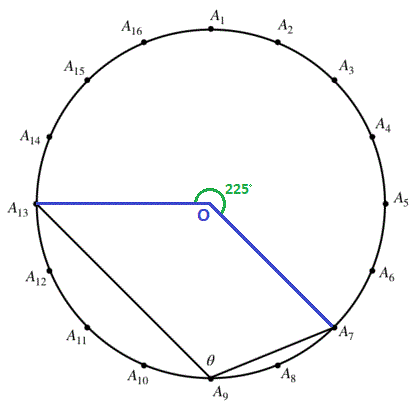
Then ∠ A 1 3 O A 7 (the angle that subtends the major arc) is 1 6 1 0 ⋅ 3 6 0 ° = 2 2 5 ° , and since an inscribed angle subtended by two points is half the central angle subtended by the same two points, θ = 2 1 ⋅ 2 2 5 ° = 1 1 2 . 5 ° .
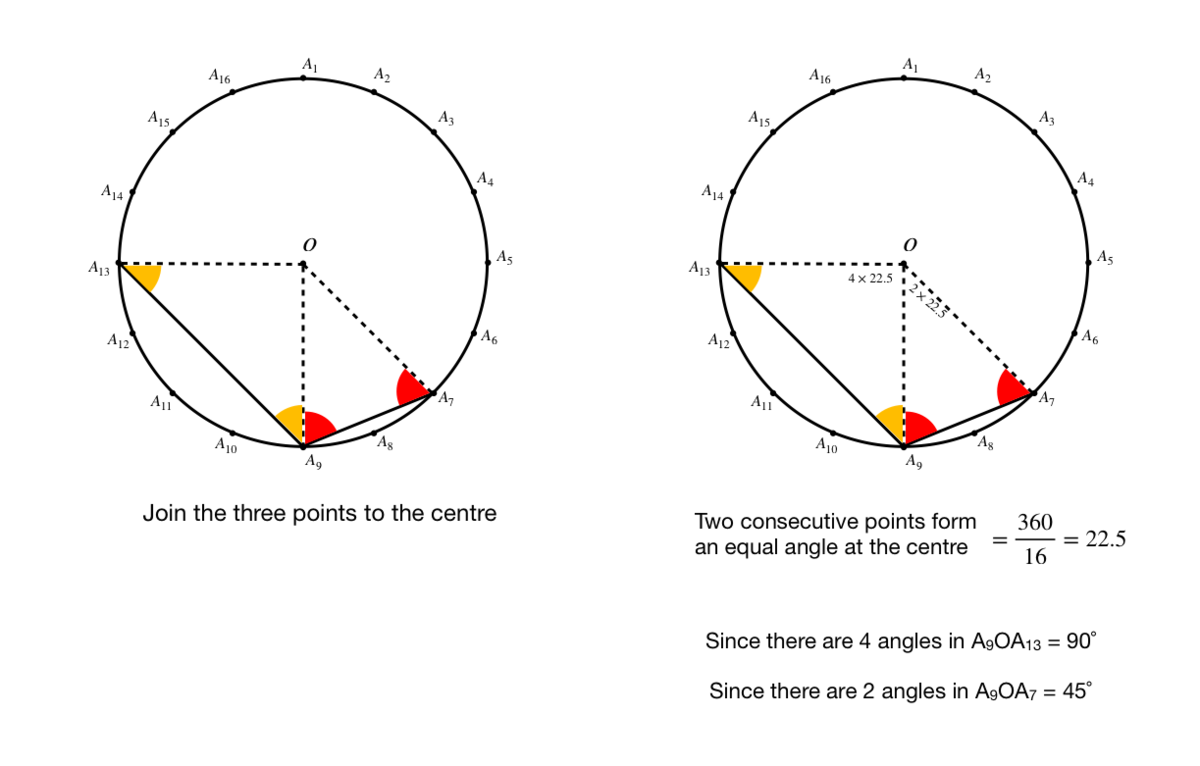
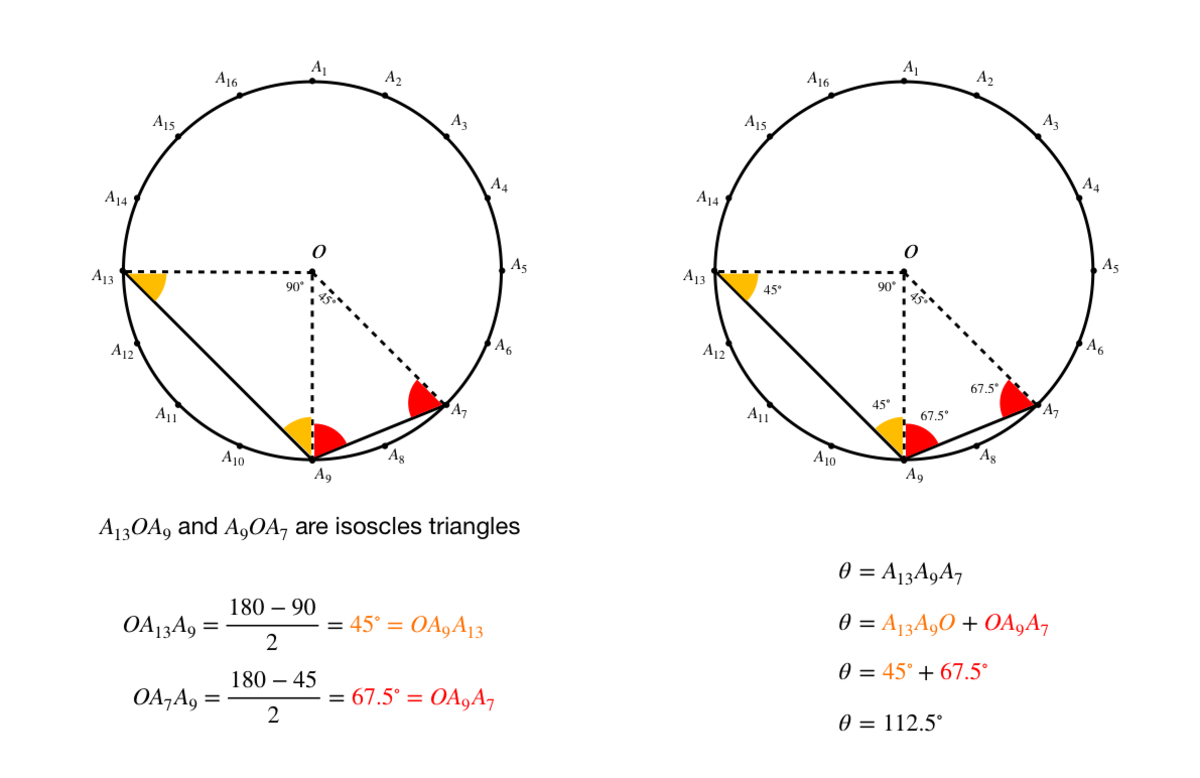
Choose any point from A 1 4 to A 6 (I have chosen A 2 for convenience) to make A 2 A 7 A 9 A 1 3 a cyclic quadrilateral , so that we can use its properties. Let the center of the circle be O . Then ∠ A 7 O A 1 3 = 1 6 6 × 3 6 0 ∘ = 1 3 5 ∘ . For the same chord the angle it extends at the circumference is half that of the angle at the center. Therefore ∠ A 7 A 2 A 1 3 = 2 1 3 5 ∘ = 6 7 . 5 ∘ . Since the opposite angles of a cyclic quadrilateral add to 1 8 0 ∘ , ∠ A 7 A 9 A 1 3 = 1 8 0 ∘ − 6 7 . 5 ∘ = 1 1 2 . 5 ∘ .