18 - 24 - 30 triangle
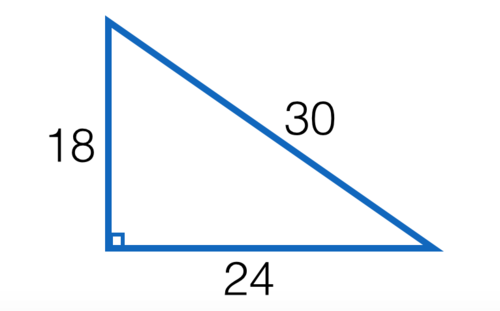 What is the area of a triangle with side lengths 18, 24, and 30?
What is the area of a triangle with side lengths 18, 24, and 30?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Moderator note:
Good observation that the triangle is similar to a favorite 3 − 4 − 5 right triangle.
We can calculate that the area of the 3 − 4 − 5 triangle is 6. What would the area of this similar triangle be?
A² = s(s-a)(s-b)(s-c) A²= (18+24+30)/2 (s-a)(s-b)(s-c) A²= 33,5 (33,5-18)(33,5-24)(33,5-30) A² = 33,5 . 15,5 . 9,5 . 3,5 A²= 46656 A= 216
Since the lengths of the triangle have a GCF not equal to 1 then we can reduce it by the principle of similar triangles, this would give us the "simplest" lengths of ( 9 , 1 2 , 1 5 ) . There are several approaches you can work on, here are some:
(1) Since the lengths satisfy the pythagorean relation, a 2 + b 2 = c 2 , we can proceed to A = ( 1 / 2 ) ( b h ) with the two shorter sides be base or height.
A = ( 1 / 2 ) ( 9 ) ( 1 2 ) A = 5 4 and since the side ratio of the original triangle and the simplest triangle, the ratios of their areas is equal to its square, thus,
A = 5 4 ( 4 ) = 2 1 6
(2) Since we were given lengths of sides of the triangle, we can use Heron's Formula: A = ( s ) ( s − a ) ( s − b ) ( s − c ) where s is the semi perimeter of the triangle.
s = ( 1 / 2 ) ( 1 8 + 2 4 + 3 0 )
s = 9 + 1 2 + 1 5
s = 3 6
Thus,
A = ( 3 6 ) ( 3 6 − 1 8 ) ( 3 6 − 2 4 ) ( 3 6 − 3 0 )
A = 6 6
A = 2 1 6
Which agrees with (1).
I committed some errors, on ( 9 , 1 2 , 1 5 ) sorry about that.
a=18,b=24,c=30 Area=Sqrt[s(s-a)(s-b)(s-c) where 2s=a+b+c s=36, s-a=18, s-b=12, s-c=6 Area= sqrt[36x18x12x6]= sqrt[6x6x6x3x6x2x6]=6x6x6=216
we can do it by either the herons formula or the simple formula... both ways, the area is 216
Clearly 2 4 2 + 1 8 2 = 3 0 2
Hence it is a Right-angled Triangle
So, Area = 2 1 × b a s e × h e i g h t = 2 1 × 1 8 × 2 4 = 2 1 6
18 , 24 , 30 is a triangle , then by divide all by 6 we get 3 , 4 , 5 as we know these lengths belong to Right-angled triangle , then area of that triangle will be ( 1/2 * 24 ) * 18 = 216 answer is = 216
by heorn's formula :_ [s(s-a)(s-b)(s-c)]^1/2 we get
semi perimeter (S):_ a+b+c/2 (where a,b,c are lengths of sides of triangle)
30+18+24/2= 36
by the heron's formula :- put the value of s 'a'b'c
area of triangle is :_ [36(36-18)(36-24)(36-30)]^1/2 = 216
there are 3 sides given in the triangle so we will find the area by Heron's Formula . Let a=18 , b=24 , c=30, S = a+b+c / 2 = 18+24+30 / 2 = 36 Area = \sqrt{s(s-a)(s-b)(s-c)} =\sqrt{36(36-18)(36-24)(36-30)} =\sqrt{36 * 18 * 12 * 6} =\sqrt{46656} =216
From the side lengths 18, 24, and 30, we can see that it forms the ratio of 3:4:5
Hence, we can deduce that this is a right angled triangle, with 18 and 24 forming the right angle. To find the area, we do (18*24)/2=216 and we get the answer.