1821 Japanese Sangaku

Given a right triangle of sides 3 , 4 , 5 , a blue ellipse is inscribed, tangent to all three sides, with its major axis parallel with the hypotenuse. Three identical red circles are inscribed, two of them inside the blue ellipse and tangent to each other, the third tangent to the blue ellipse also, but tangent to the two shorter sides of the triangle.
Find the diameter D of the identical red circles, which is slightly greater than 1 . Enter your answer as ⌊ 1 0 0 0 D ⌋
The answer is 1070.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Your explanation and solution just made this problem one of the best I've posted, being that it's based on an old Japanese sangaku classic. There shouldn't be any doubt that this is the correct answer, without having to delve into the insanely complex mathematics in that paper, which is really about finding the relationship between the sides a , b of the right triangle and the radius r of the red circles. This is a readily solvable problem if it's about finding a practical means of approximating the answer. Kudos, Mark, you really have a way of nailing difficult problems such as this. Your solutions are always excellent.
I had decided to tackle and post this problem because of that 2011 paper!
Log in to reply
Thank you.
Well, to be fair, the paper is about finding alebraic solutions. The whole TOP business is, of course, just a matter of finding polynomial remainders lots of times.
My formula for λ is a quartic, and quartics have exact solutions. It might be interesting to try to find the exact expression for the key value of λ , and hence an explicit expression for X in terms of β . That is for another day, perhaps...
The diameter of the red circles works out to 1 . 0 7 0 7 6 0 7 2 0 . . . , or radius of 0 . 5 3 5 3 8 0 3 6 0 . . .
The major and minor axes of the blue ellipse works out to 1 . 8 1 4 4 5 0 1 5 0 . . . , and 0 . 5 6 3 1 9 8 2 3 3 . . .
Edit: After seeing Mark's posted numbers, I pushed my approximation to D = 1 . 0 7 0 7 6 0 7 2 0 1 8 3 0 4 3 . . .
Refer to the figure below, showing a right triangle of sides in proportions of 3 , 4 , 5 , a blue ellipse centered at the origin ( 0 , 0 ) , and red and green unit circles. The center of the green unit circle is ( x 0 , y 0 ) . The major axis of the blue ellipse is p while the minor axis is p q . Then if the blue ellipse is tangent to the right triangle, the red unit circles tangent to it and each other, and the green unit circle is tangent to the right triangle, then the following must be true
p = q 1 − q 2 1
x 0 = 5 1 + 2 5 q 1 − q 2 1 ( 9 + 1 6 q 2 2 7 + 4 8 q 2 − 1 6 + 9 q 2 6 4 + 3 6 q 2 )
y 0 = − 5 7 + 2 5 q 1 − q 2 1 ( 1 6 + 9 q 2 4 8 + 2 7 q 2 + 9 + 1 6 q 2 3 6 + 6 4 q 2 )
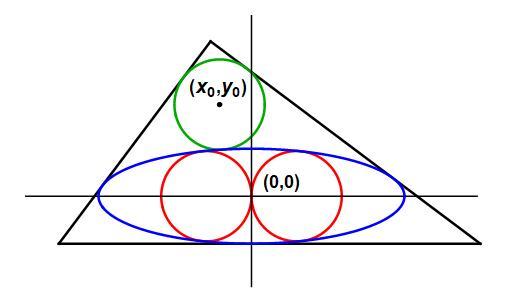
Then we solve the following simple equation for x
y 0 − 1 − ( x − x 0 ) 2 = q p 2 − x 2
...and that's when things explode. But q can still be worked out, q = 0 . 3 1 0 3 9 6 0 9 0 5 8 1 2 5 6 0 2 9
This is how bad it gets when it's done this way. Let
a = ( q 2 − 1 ) 2
b = 2 5 q 4 ( 5 q 3 + 1 − q 2 ( 4 9 q 2 + 1 6 − 3 1 6 q 2 + 9 ) − 5 q )
c = 6 2 5 q 2 ( q 2 − 1 ) 1 ( 3 6 5 0 q 6 − 1 1 4 8 q 4 − 8 ( 1 2 9 q 2 + 1 6 1 6 q 2 + 9 + 6 1 3 ) q 2 + 2 0 1 − q 2 ( 3 3 9 q 2 + 1 6 + 1 9 1 6 q 2 + 9 ) q + 9 6 9 q 2 + 1 6 1 6 q 2 + 9 + 2 0 1 − q 2 ( 1 7 9 q 2 + 1 6 + 3 1 1 6 q 2 + 9 ) q 3 − 2 5 9 8 )
d = − 1 2 5 q 3 ( q 2 − 1 ) 2 4 ( 2 5 q 7 − 7 6 q 5 + 3 5 1 − q 2 ( 1 6 q 2 + 9 − 2 9 q 2 + 1 6 ) q 2 + ( 2 9 q 2 + 1 6 1 6 q 2 + 9 + 9 9 ) q + 5 1 − q 2 ( 3 1 6 q 2 + 9 − 4 9 q 2 + 1 6 ) + 5 1 − q 2 ( 6 9 q 2 + 1 6 − 1 6 q 2 + 9 ) q 4 − 2 ( 9 q 2 + 1 6 1 6 q 2 + 9 + 2 4 ) q 3 )
e = 6 2 5 q 4 ( q 2 − 1 ) 2 1 ( 6 2 5 q 8 − 1 3 5 0 q 6 + 2 ( 5 2 9 q 2 + 1 6 1 6 q 2 + 9 + 2 5 4 9 ) q 2 − 5 0 0 1 − q 2 ( 9 q 2 + 1 6 + 1 6 q 2 + 9 ) q + 5 0 0 1 − q 2 ( 9 q 2 + 1 6 + 1 6 q 2 + 9 ) q 5 − ( 2 0 0 9 q 2 + 1 6 1 6 q 2 + 9 + 1 8 7 3 ) q 4 − 2 0 1 − q 2 ( 3 3 9 q 2 + 1 6 + 1 9 1 6 q 2 + 9 ) q 3 + 6 2 5 )
then solve for q such that
0 = 2 2 / 3 a 2 3 ( 2 7 ( a d 2 + b 2 e ) − 9 c ( 8 a e + b d ) + 2 c 3 ) 2 − 4 ( 1 2 a e − 3 b d + c 2 ) 3 − 7 2 a c e + 2 7 a d 2 + 2 7 b 2 e − 9 b c d + 2 c 3 + 3 ( 2 7 ( a d 2 + b 2 e ) − 9 c ( 8 a e + b d ) + 2 c 3 ) 2 − 4 ( 1 2 a e − 3 b d + c 2 ) 3 − 7 2 a c e + 2 7 a d 2 + 2 7 b 2 e − 9 b c d + 2 c 3 2 3 2 a 2 ( 1 2 a e − 3 b d + c 2 ) + 2 2 2 / 3 a 3 ( 2 7 ( a d 2 + b 2 e ) − 9 c ( 8 a e + b d ) + 2 c 3 ) 2 − 4 ( 1 2 a e − 3 b d + c 2 ) 3 − 7 2 a c e + 2 7 a d 2 + 2 7 b 2 e − 9 b c d + 2 c 3 + 3 ( 2 7 ( a d 2 + b 2 e ) − 9 c ( 8 a e + b d ) + 2 c 3 ) 2 − 4 ( 1 2 a e − 3 b d + c 2 ) 3 − 7 2 a c e + 2 7 a d 2 + 2 7 b 2 e − 9 b c d + 2 c 3 4 3 2 a ( 1 2 a e − 3 b d + c 2 ) − 8 a c + 3 b 2 3 3 a ( 8 a 2 d − 4 a b c + b 3 ) + 8 a 2 c − 3 a b 2
How did you solve it?
Log in to reply
Set it up so that a single variable q = a b (ratio of minor and major axes of the blue ellipse) determined the space between the outlier red circle and the blue ellipse, and then numerically found the value required to reduce this space to 0 as closely as possible. I had just one "knob" to work with. Unfortunately, the expression used in the last step suddenly becomes really messy. It is surprisingly difficult to determine when a circle and an ellipse become tangent.
Using the notation of the referred-to paper, we have a = 5 , b = 3 , c = 4 , h = 2 a c 2 − b 2 , k = a b c , m = c b . If β is the semi-major axis of the ellipse, then the coordinates ( x 0 , y 0 ) of the centre of the ellipse are given by x 0 = h − β k ( h − 2 β ) y 0 = h − β while the semi-major axis α of the ellipse, and its eccentricity e are given by α = m 1 ( m x 0 − y 0 ) 2 − β 2 e = ( m x 0 − y 0 ) 2 − β 2 ( m x 0 − y 0 ) 2 − ( m 2 + 1 ) β 2 while the radius of the three circles is r = e β while the coordinates of the centre of the bottom circle are ( x 1 , y 1 ) where x 1 = a r ( c − b ) y 1 = a r ( c + b ) These conditions (for a suitable range of values of β ) ensure that the ellipse is tangent to all three sides of the triangle, and that the two circles of radius r are mutually tangent, and both tangent to the ellipse, and also that the bottom circle is tangent to the bottom two sides of the triangle. We now need to choose β so that the bottom circle is tangent to the ellipse. The important point is that all the parameters of the problem have been expressed in terms of β (and a , b , c ). There is only one degree of freedom for any right-angled triangle.
My aim is to find a way of solving this problem that does not descend into the involved manipulation of three different quartics required in the paper. If a simpler approach can be found, a numerical solution will be relatively easy.
We want to determine the value of β such that the shortest distance from the ellipse α 2 x 2 + β 2 y 2 = 1 to the point ( x 0 − x 1 , y 0 − y 1 ) is equal to r . Applying the method of Lagrange multipliers, the shortest distance from the point to the ellipse is equal to X = ( α 2 + λ ) 2 λ 2 ( x 0 − x 1 ) 2 + ( β 2 + λ ) 2 λ 2 ( y 0 − y 1 ) 2 where λ is the positive value such that ( α 2 + λ ) 2 α 2 ( x 0 − x 1 ) 2 + ( β 2 + λ ) 2 β 2 ( y 0 − y 1 ) 2 = 1 (the maximum distance from the point to the ellipse is obtained by finding the negative solution of λ ).
The equation X = r can be solved numerically, and we obtain β = 0 . 5 6 3 1 9 8 2 3 3 1 2 5 2 9 6 8 , α = 1 . 8 1 4 4 5 0 1 5 0 0 3 4 5 4 6 7 , e = 0 . 9 5 0 6 0 7 3 1 4 8 0 0 3 1 9 , r = 0 . 5 3 5 3 8 0 3 6 0 0 9 1 5 2 2 5 , and hence D = 1 . 0 7 0 7 6 0 7 2 0 1 8 3 0 4 5 , so that ⌊ 1 0 0 0 D ⌋ = 1 0 7 0 .