1846 Sangaku Maximum
Two unit squares, black and blue, are inscribed inside a trapezoid.
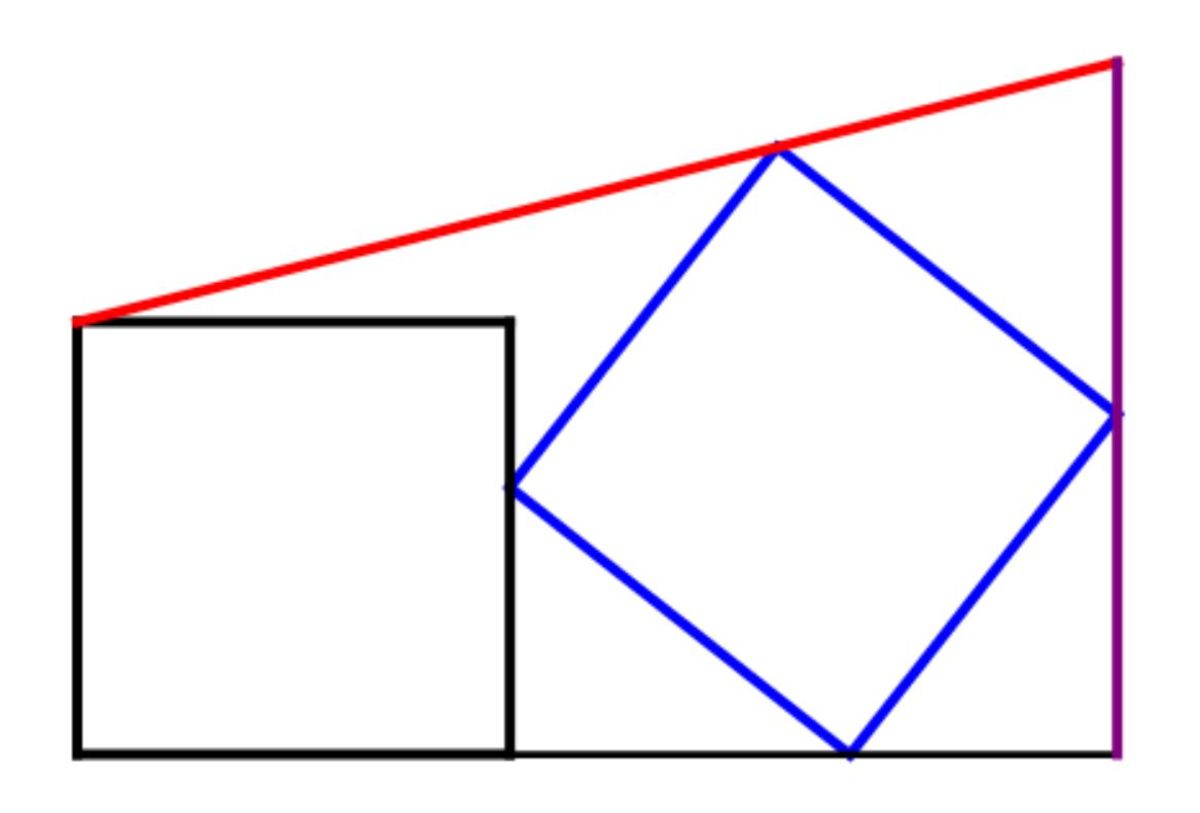
The black square shares a right angle corner and left side with the trapezoid. The blue square is rotated in such a way as to maximize the length of the vertical right side (purple) of the trapezoid.
This length can be expressed as 1 + a b − c , where a , b , and c are square-free positive integers.
What is the sum a + b + c ?
The answer is 37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
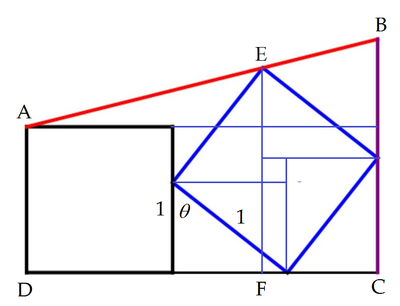
Label the trapezoid as A B C D and altitude of the top vertex of the blue unit square as E F ; and let the angle a side of the blue square makes with the vertical be θ as shown.
Then E F = sin θ + cos θ , D F = 1 + cos θ , and D C = 1 + sin θ + cos θ , then
E F − 1 B C − 1 ⟹ B C h ⟹ max ( h ) = D F D C = 1 + D F D C ( E F − 1 ) = 1 + 1 + cos θ ( sin θ + cos θ + 1 ) ( sin θ + cos θ − 1 ) = 1 + 1 + cos θ 2 sin θ cos θ = 1 + 1 + 2 cos 2 2 θ − 1 2 ( 2 sin 2 θ cos 2 θ ) ( 2 cos 2 2 θ − 1 ) = 1 + 2 sin θ − 2 tan 2 θ = 1 + 1 + t 2 4 t − 2 t = 1 + 1 + t 2 2 t ( 1 − t 2 = 5 − 1 2 5 − 2 ( 3 − 5 ) = 1 + ( 5 − 1 ) ( 5 + 1 ) 2 5 − 2 ( 3 − 5 ) ( 5 + 1 ) = 1 + 5 − 2 ( 5 − 1 ) = 1 + ( 5 − 2 ) ( 6 − 2 5 ) = 1 + 1 0 5 − 2 2 Let B C = h Let t = tan 2 θ See note: h is maximum, when t = 5 − 2
Therefore a + b + c = 1 0 + 5 + 2 2 = 3 7 .
Note: To find max ( h ) , we first find t , when d t d h = 0 .
d t d h ⟹ ( 1 + t 2 ) 2 4 − 4 t 2 2 − 2 t 2 t 4 + 4 t 2 − 1 ⟹ t = ( 1 + t 2 ) 2 4 ( 1 + t 2 ) − 4 t ( 2 t ) − 2 = 2 = t 4 + 2 t 2 + 1 = 0 = 5 − 2 Equating to zero
Draw in these lines and label the diagram as follows:
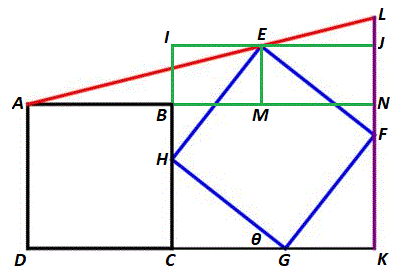
From right △ H C G and G H = 1 , C G = sin θ and C H = cos θ . By symmetry, C G = H I = E J = F K = sin θ and C H = E I = F J = G K = cos θ .
△ A M E ∼ △ A N L by AA symmetry, so A N L N = A M E M . Letting y = L K ,
-
L N = L K − N K = y − 1
-
A N = C D + C G + K G = sin θ + cos θ + 1
-
E M = B I = C H + H I − B C = sin θ + cos θ − 1
-
A M = A B + B M = A B + E I = sin θ + 1
Substituting these into the ratio gives sin θ + cos θ + 1 y − 1 = sin θ + 1 sin θ + cos θ − 1 which simplifies to y = sin θ + 1 2 sin θ cos θ + 1 .
The maximum of y = L K occurs when the derivative y ′ is zero, therefore, y ′ = ( sin θ + 1 ) 2 2 ( 1 + sin θ ) ( cos 2 θ − sin 2 θ ) − 2 sin θ cos 2 θ = 0 . Using the identity cos 2 θ = 1 − sin 2 θ , this simplifies to ( sin θ + 1 ) ( sin 2 θ + sin θ − 1 ) = 0 , which has one positive solution of sin θ = 2 5 − 1 .
This makes cos θ = 1 − sin 2 θ = 2 5 − 1 , which makes the maximum of L K to be y = sin θ + 1 2 sin θ cos θ + 1 = 1 + 1 0 5 − 2 2 , so that a = 1 0 , b = 5 , c = 2 2 , and a + b + c = 3 7 .
It's interesting to see that the sides of △ H C G end up being in a geometric progression with hints of the golden ratio.
Yeah, that is interesting. H G × H C = C G × C G . Hmm....
The only such right angled triangle (up to scaling). Seems weird it doesn't come up more often.
It is the equation for the golden ratio: x 2 + x = 1 . I just found out that it is called a Kepler triangle.
Is there any non-trig solution??
Let the angle of bottom left side of right square as x, determine the slope M(x) of inclined line of trapezoid: M=[{(2^0.5)sin(x+pi/4)-1}/{1+cos(x)-(2^0.5)cos(x+pi/4)}], and the vertical right side H of trapezoid: H=[1+{1+sin(x)+cos(x)}M]. Maximum of H(x) gives H=1+[10{(5)^0.5}-22]^0.5. Therefore, a+b+c=10+5+22 Answer=37
Let us define the tilting angle as x and let us mark vertices A , B , C , D and E as in figure below. Let us also call the purple side as y .
We will have:
y = 1 + D E
Notice also that:
B C = cos ( x ) + sin ( x ) − 1
A B = 1 + cos ( x )
A D = cos ( x ) + sin ( x ) + 1
Triangles Δ A B C and Δ A D E are similar, so:
B C D E = A B A D
D E = 1 + cos ( x ) ( cos ( x ) + sin ( x ) − 1 ) ( cos ( x ) + sin ( x ) + 1 )
D E = 1 + cos ( x ) ( cos ( x ) + sin ( x ) ) 2 − 1
D E = 1 + cos ( x ) sin ( 2 x )
y = 1 + 1 + cos ( x ) sin ( 2 x )
Differentiating y with respect to x and making it equal to 0 :
d x d y = ( 1 + cos ( x ) ) 2 2 cos ( 2 x ) ( 1 + cos ( x ) ) − sin ( 2 x ) ( − sin ( x ) ) = 0
d x d y = ( 1 + cos ( x ) ) 2 2 ( 2 cos 2 ( x ) − 1 ) ( 1 + cos ( x ) ) + 2 sin 2 ( x ) cos ( x ) = 0
d x d y = ( 1 + cos ( x ) ) 2 2 ( 2 cos 2 ( x ) − 1 ) ( 1 + cos ( x ) ) + 2 ( 1 − cos 2 ( x ) ) cos ( x ) = 0
Since 0 ≤ x ≤ 2 π , 1 + cos ( x ) = 0 . So:
cos 3 ( x ) + 2 cos 2 ( x ) − 1 = 0
( cos ( x ) + 1 ) ( cos 2 ( x ) + cos ( x ) − 1 ) = 0
cos ( x ) = − 1 is impossible since 0 ≤ x ≤ 2 π . The other two solutions are cos ( x ) = − 2 1 + 5 ≈ − 1 . 6 1 8 , which is also impossible, and:
cos ( x ) = 2 5 − 1
Which leads to:
sin ( x ) = 2 2 5 − 2
So:
y = 1 + 1 + cos ( x ) sin ( 2 x )
y = 1 + 1 + cos ( x ) 2 sin ( x ) cos ( x )
y = 1 + 5 + 1 ( 2 5 − 2 ) ( 5 − 1 )
Multiplying above and below by 5 − 1 :
y = 1 + 4 ( 2 5 − 2 ) ( 6 − 2 5 )
y = 1 + 4 ( 2 5 − 2 ) ( 6 − 2 5 ) 2
y = 1 + 1 6 1 6 0 5 − 3 5 2
y = 1 + 1 0 5 − 2 2
So:
a = 1 0 , b = 5 , c = 2 2 → a + b + c = 3 7