1973rd non-perfect square

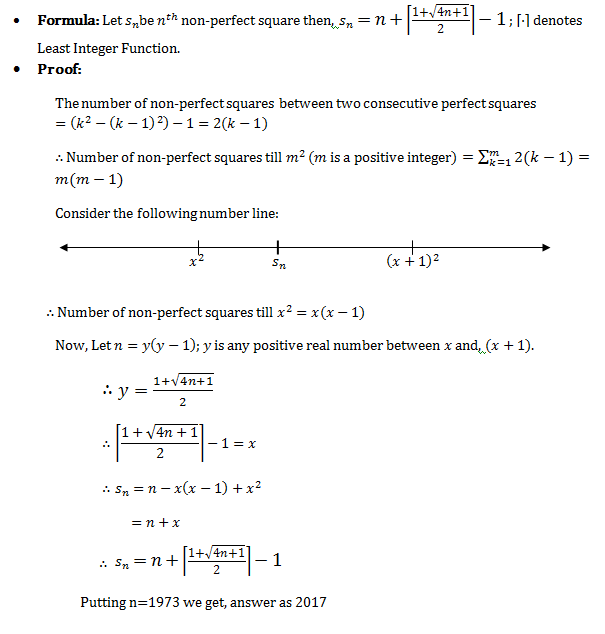
Let $q(n)$ be the $n$ th non-perfect integer. Then the sequence of non-perfect integers up to $q(n)=k^2 +1$ , where $k^2$ is the $k$ th perfect square is as follows:

$\begin{aligned} \{ q(n) \} & = \underbrace{ {\color{#D61F06}\cancel 1}, 2, 3, {\color{#D61F06}\cancel 4}, 5, 6, 7, 8, {\color{#D61F06}\cancel 9}, 10, \cdots {\color{#D61F06}\cancel {k^2}}, k^2+1}_{k^2+1-k \text{ terms}} \\ \implies n & = k^2 - k + 1 \\ q(k^2-k+1) & = k^2 + 1 \end{aligned}$

Now the largest perfect square smaller than 1973 is $\lfloor \sqrt {1973}\rfloor =44$ . Then, we have:

$\begin{aligned} q(k^2-k+1) & = k^2+1 & \small \color{#3D99F6} \text {Putting }k=44 \\ q(44^2-44+1) & = 44^2+1 \\ q(1893) & = 1937 \\ q(1893+80) & = 1937+80 \\ q(1973) & = \boxed{2017} \end{aligned}$

It is much easier to just consider N(x) = x - floor( sqrt(x)) which is equal to the number of non-squares less than or equal to x. Then it's trivial to check that N(44²) = 1936-44 < 1973 and N(45²) > 1973 so we seek x between 44² and 45² such that x - 44 = 1973. Thus, x = 2017.