1997 Korean CSAT problem(Geometry)
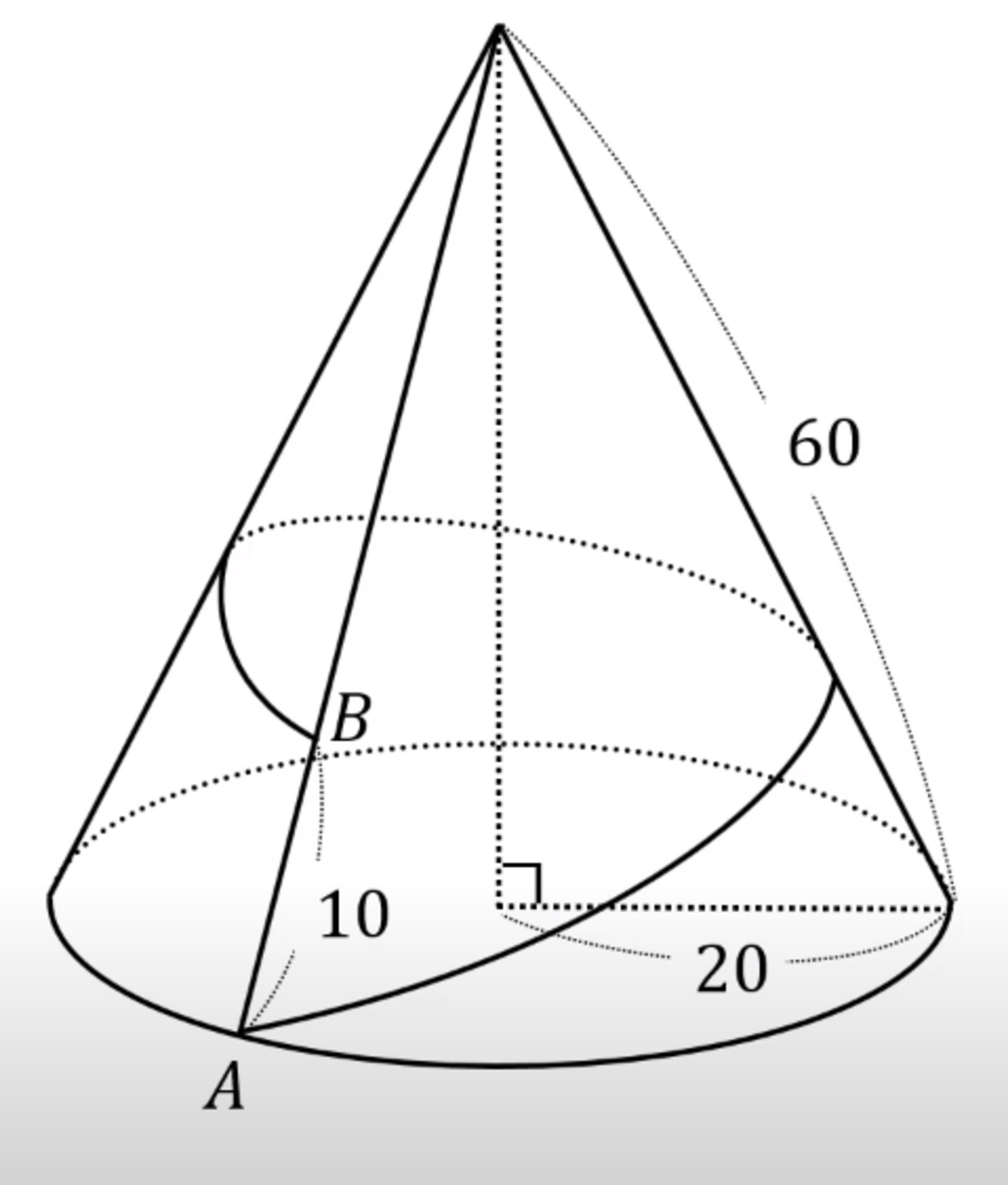 This diagram represents a circular cone-shaped mountain. If you build, for a sightseeing train around the mountain, the
shortest
track that starts at point A and ends at point B, the track will start going uphill, but later going downhill. How long is the downhill track?
This diagram represents a circular cone-shaped mountain. If you build, for a sightseeing train around the mountain, the
shortest
track that starts at point A and ends at point B, the track will start going uphill, but later going downhill. How long is the downhill track?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@A Former Brilliant Member , you have to mentioned that it is the shortest track from A to B as there are infinitely many tracks between A and B.
The full solution is described in Mind Your Decisions' blog .
In summary, unroll the cone to get a flat, circular sector. Its radius is 60, but the circular sector's circumference is 4 0 π . Therefore the central angle θ = 6 0 4 0 π = 1 2 0 º . Now place A on one vertex, and B on the other vertex 10 units up, so the other side is 50 units. The length of AB is therefore 1 0 9 1 using the cosine rule. The downhill portion of this line is the shorter part intersected by the perpendicular bisector. Now using the Pythagorean theorem, 6 0 2 − ( 1 0 9 1 − x ) 2 = 5 0 2 − x = h 2 , where x is the length of the downhill portion and h is the altitude. The x 2 terms cancel, leaving a linear equation which gives x = 9 1 4 0 0 .
Let the vertex of the cone be C . Cut open the cone along a straight line from A to C via B . Place the cone surface flat. Since C is equidistance, 6 0 , from the base circle A A ′ , the flat surface area is a circle sector of radius 6 0 . As the base circle has a circumference of 2 π × 2 0 = 4 0 π . The angle of the sector ∠ A C A ′ = 6 0 4 0 π = 3 2 π r a d or 1 2 0 ∘ .
The shortest track between A and B is the straight line joining A and B on the flat surface. Let any point of A B be P . The shorter the length C P , the higher the point P on the track. Initially the length of C P is decreasing as the track is going uphill, until C P is perpendicular to A B . There, the track has reached its highest point and after that it goes downhill. So we need to find th lenght of B P when C P is perpendicular to A B .
Since A ′ C = 6 0 and A ′ B = 1 0 , B C = 5 0 . By cosine rule ,
A B 2 ⟹ A B = B C 2 + C A 2 − 2 ⋅ B C ⋅ C A ⋅ cos 1 2 0 ∘ = 5 0 2 + 6 0 2 − 2 ⋅ 5 0 ⋅ 6 0 ( − 2 1 ) = 1 0 9 1
By sine rule ,
C A sin B sin B ⟹ B P = A B sin C = A B sin C ⋅ C A = 2 ⋅ 1 0 9 1 6 0 3 = 9 1 2 7 = B C ⋅ cos B = 5 0 1 − 9 1 2 7 = 9 1 4 0 0