2 circles tangent to each other... (Application of Angle Bisector)

Geometry Level 3

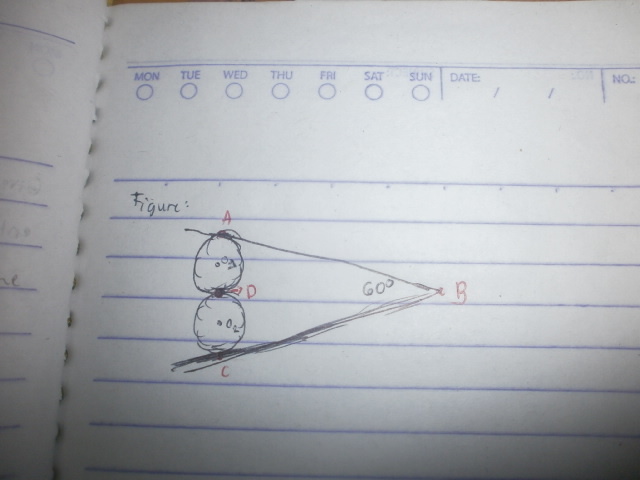Given 2 $congruent$ circles w/ center $O_{1}$ and $O_{2}$ is tangent to each other and circle $O_{1}$ is tangent to AB and Circle $O_{2}$ is tangent to CB. If $\angle ABC$ is $60 degrees$ and there is 1 chord in Circle $O_{1}$ named $AD$ such that, it is tangent to $AB$ as shown in the fig. Given that $AD$ is $15 cm.$ , find the $Area(Circle O_{1}) + Area(Circle O_{2}$ .

$-----$

Assumptions: Use $\pi = 3.14$ or $\cfrac{22}{7}$ or $3.1416$

Note:

1) Round down your answer to a whole number $i.e. 1.222222... = 1, 300.1222222 = 300, 8999.8888... = 8999$

2) Point $D$ is found between the 2 circles. (point of tangency)

3) $AD$ and $CD$ are not radii.

The answer is 378.

1 solution

Christian Daang
Jan 24, 2015

By using Law of Sines in Triangle $AO_{1}D$ ,

$\cfrac{sin 150}{15} = \cfrac{sin 15}{r}$

-> $\cfrac{{1}/{2}}{15} = \cfrac{\cfrac{\sqrt{6} - \sqrt{2}}{4}}{r}$

-> $r = \cfrac{15(\sqrt{6}-\sqrt{2}}{2}$

Since Circle $O_{1}$ ~ Circle $O_{2}$ , then, Area(Circle $O_{1}$ ) ~ Area(Circle $O_{2}$ )

Area(Circle $O_{1}$ = $(\cfrac{15(\sqrt{6}-\sqrt{2}}{2})^{2} * \pi$

= $225\pi * (2-\sqrt{3}$ sq. units.

$\therefore$ ,

Area $Circle O_{1}$ + Area $Circle O_{2}$ = 2* $225\pi * (2-\sqrt{3}$ which is approximately equal to $\boxed{378 sq. units}$

2 circles tangent to each other... (Application of Angle Bisector)

The answer is 378.

1 solution

0 pending reports