2 circles
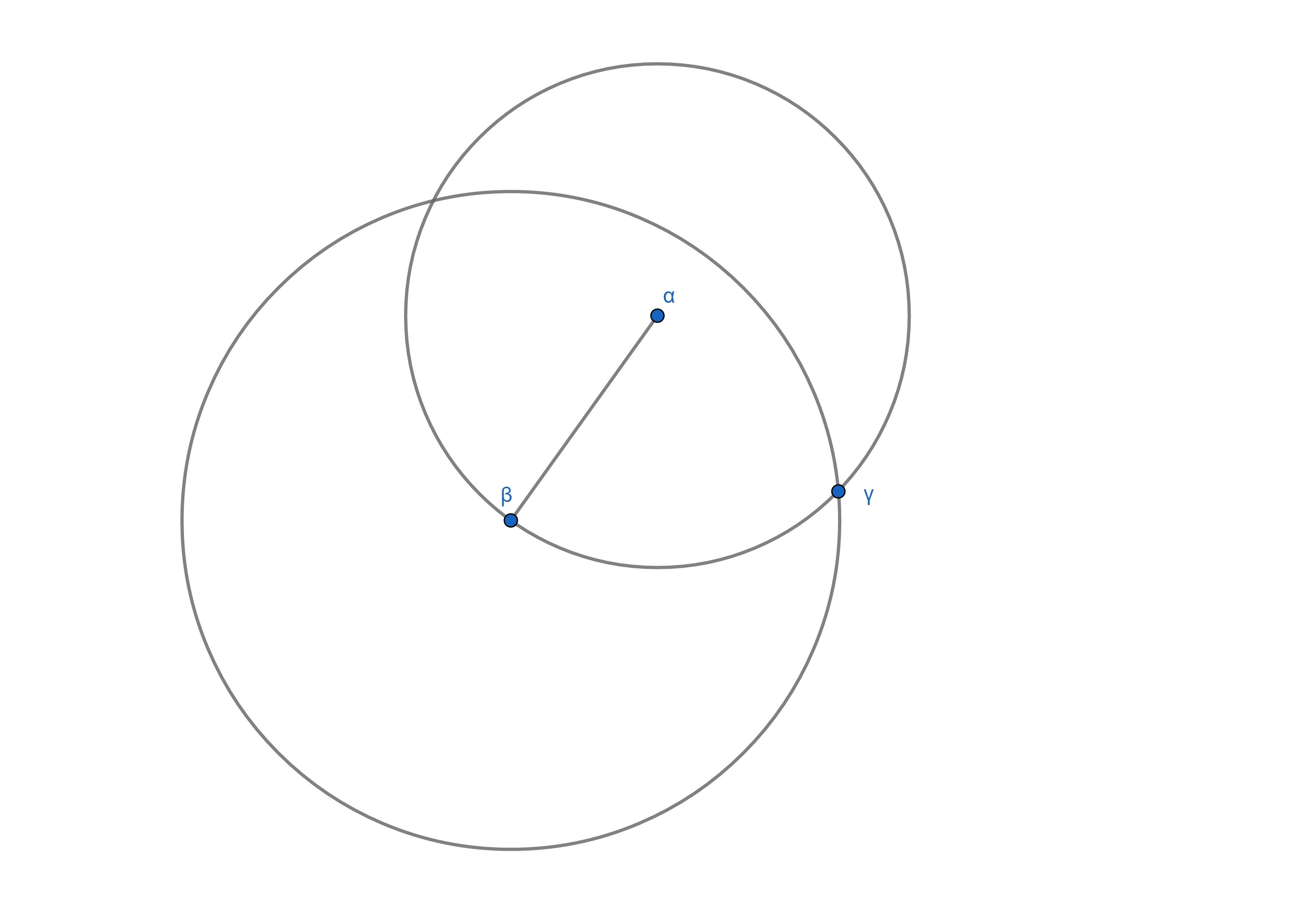 A circle with center point
is placed on another circle with center point
such that it goes through an arbitrary point
on the circle with center point
. What is the probability that the circle with center point
and the line segment
intersect?
A circle with center point
is placed on another circle with center point
such that it goes through an arbitrary point
on the circle with center point
. What is the probability that the circle with center point
and the line segment
intersect?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Call the other intersection point of the two circles γ ′ . Now move γ (and γ ′ ) close enough to β so that the circle with center β goes through α . At that position, both circles have equal radii, and α β = α γ = β γ so △ α β γ is equilateral making arc γ β γ ′ = 3 2 π , i.e one third of the circumference of the circle with center α . Clearly for the circle with center β to intersect α β , γ has to be on that third of the circumference, so the probability is 3 1