2 equations and 3 variables?
y x + z y + x z = 7 x y + y z + z x = 9
If x , y , z are non zero real numbers such that they satisfy the equations above, find the value of: y 3 x 3 + z 3 y 3 + x 3 z 3 − 4
The answer is 153.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Same approach!!
Take the three terms of first equation as a,b,c. Now use the identity:
a^3+b^3+c^3-3abc=[(a+b+c)^2-3(ab+bc+ca)]
This question is from KVPY , isn't it ?
H e r e ′ s a n o t h e r m e t h o d t o s o l v e i t :
G i v e n , y x + z y + x z = 7 . . . . . . . . . . . . . . . . . . . . . ( 1 ) x y + y z + z x = 9 . . . . . . . . . . . . . . . . . . . . . ( 2 )
W e k n o w t h a t , ( y x + z y + x z ) 3 = ( y x ) 3 + ( z y ) 3 + ( x z ) 3 + 3 ( x 2 y z ) + 3 ( y z x 2 ) + 3 ( y 2 x z ) + 3 ( x z y 2 ) + 3 ( z 2 x y ) + 3 ( x y z 2 ) + 6 . . . . . . . . . . . ( 3 )
On\quad multiplying\quad (1)\quad and\quad (2)\quad we\quad get,\\ \left( \frac { x }{ y } +\frac { y }{ z } +\frac { z }{ x } \right) \left( \frac { y }{ x } +\frac { z }{ y } +\frac { x }{ z } \right) =3+\frac { yz }{ x^{ 2 } } +{ \frac { x^{ 2 } }{ yz } }+\frac { xz }{ y^{ 2 } } +\frac { y^{ 2 } }{ xz } +\frac { xy }{ z^{ 2 } } +\frac { z^{ 2 } }{ xy } =63\\ 60=\frac { yz }{ x^{ 2 } } +{ \frac { x^{ 2 } }{ yz } }+\frac { xz }{ y^{ 2 } } +\frac { y^{ 2 } }{ xz } +\frac { xy }{ z^{ 2 } } +\frac { z^{ 2 } }{ xy } \\ \\ On\quad replacing\quad this\quad value\quad in\quad (3),\\ (7)^{ 3 }={ \left( \frac { x }{ y } \right) }^{ 3 }+{ \left( \frac { y }{ z } \right) }^{ 3 }+{ \left( \frac { z }{ x } \right) }^{ 3 }+180+6\\ \\ { \left( \frac { x }{ y } \right) }^{ 3 }+{ \left( \frac { y }{ z } \right) }^{ 3 }+{ \left( \frac { z }{ x } \right) }^{ 3 }=157\\ \\ \therefore \quad { \left( \frac { x }{ y } \right) }^{ 3 }+{ \left( \frac { y }{ z } \right) }^{ 3 }+{ \left( \frac { z }{ x } \right) }^{ 3 }-4=\boxed{153}
Yes, I feel like I had practiced it before from a question paper of KVPY or any such exam.
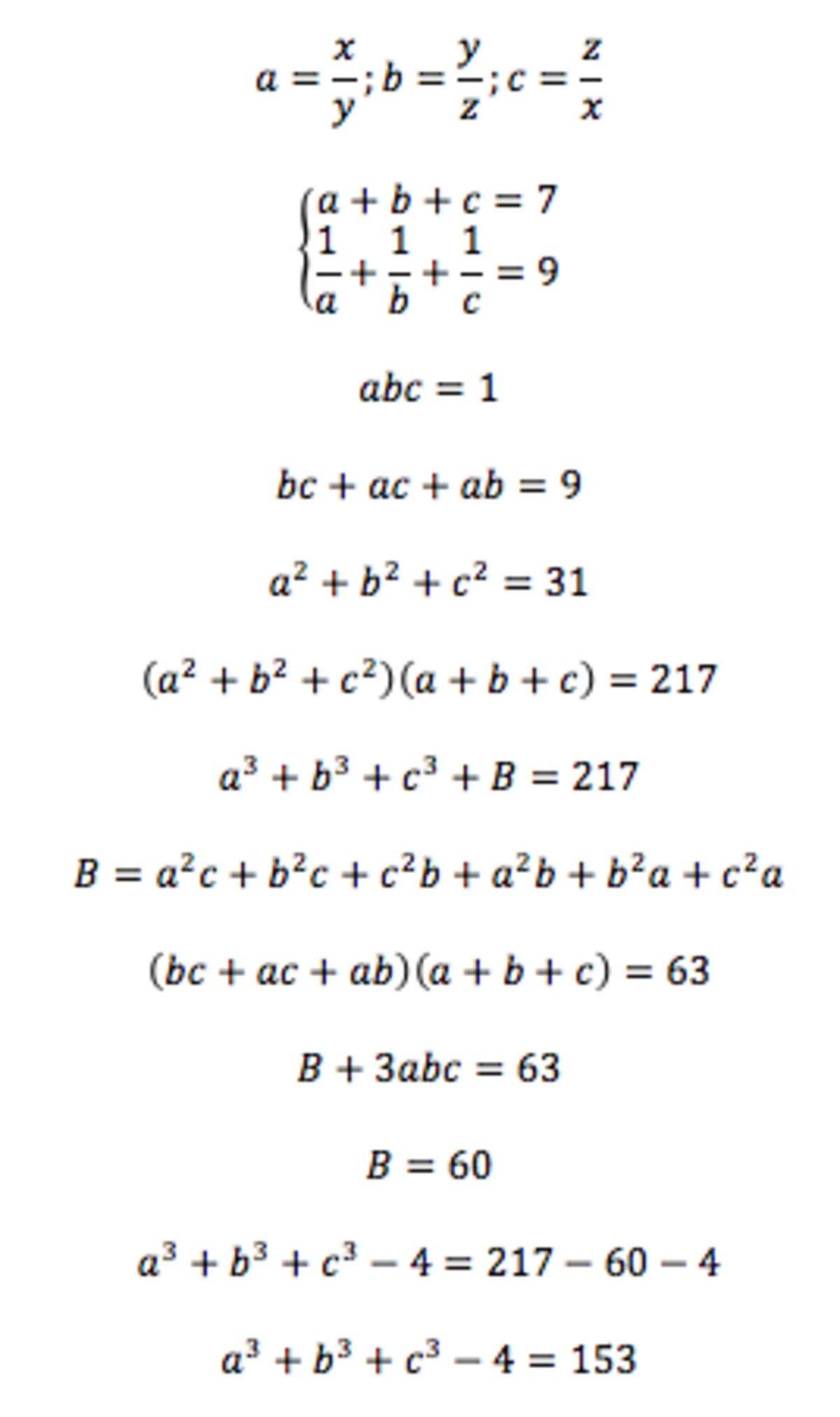
( y x + z y + x z ) 2 ⇒ y 2 x 2 + z 2 y 2 + x 2 z 2 = y 2 x 2 + z 2 y 2 + x 2 z 2 + 2 ( y x ˙ z y + z y ˙ x z + x z ˙ y x ) = y 2 x 2 + z 2 y 2 + x 2 z 2 + 2 ( z x + x y + y z ) = ( y x + z y + x z ) 2 − 2 ( z x + x y + y z ) = 7 2 − 2 × 9 = 4 9 − 1 8 = 3 1
Now, we have:
\(\begin{array} {} \dfrac {x^3}{y^3} + \dfrac {y^3}{z^3} + \dfrac {z^3}{x^3} -4 \\ = \left( \dfrac {x}{y} + \dfrac {y}{z} + \dfrac {z}{x} \right) \left( \dfrac {x^2}{y^2} + \dfrac {y^2}{z^2} + \dfrac {z^2}{x^2} \right) - \left( \dfrac {x}{z} + \dfrac {y}{x} + \dfrac {z}{y} \right) \left( \dfrac {x}{y} + \dfrac {y}{z} + \dfrac {z}{x} \right) \\ \quad + 3 \left( \dfrac {x}{y} \dot{} \dfrac {y}{z} \dot{} \dfrac {z}{x} \right) - 4 \\ = 7\times 31 - 9\times 7 + 3 - 4 = \boxed{153} \end{array}\)