2 Fast 2 Curious
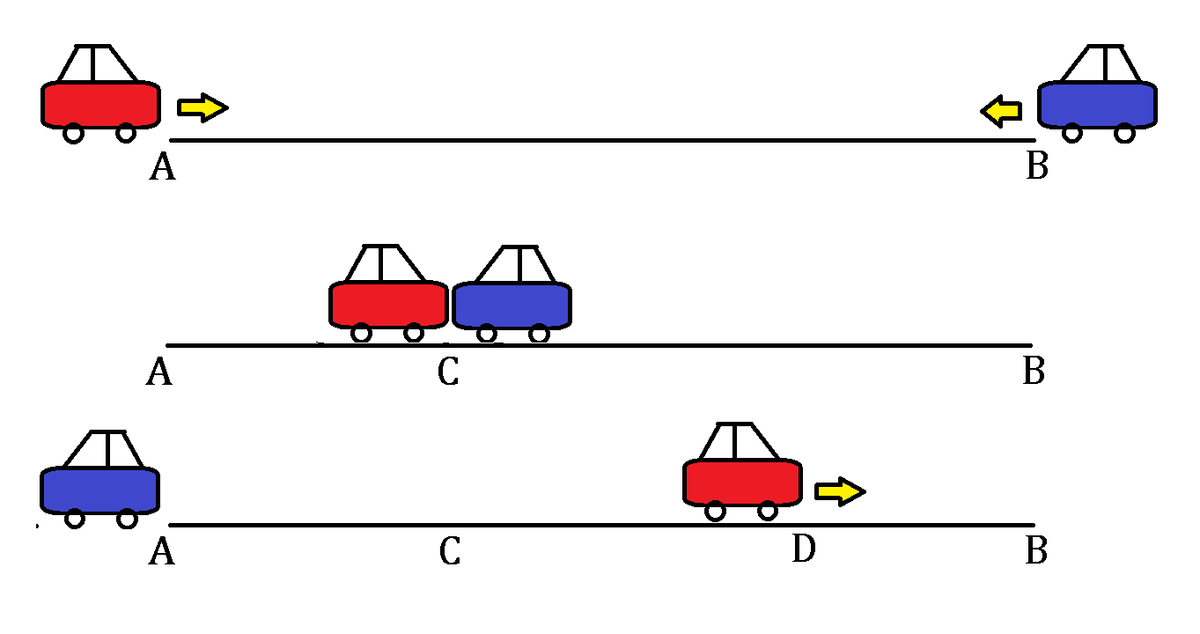
A red car and a blue car started racing towards each other at the same time from point and respectively, as shown above, where was km. long.
Then hours later, both cars met up at point with constant speeds.
Afterwards, when the blue car reached the destination at point , the red car was passing point .
If was km. long, how many more hours would the red car take to travel from point to the destination ?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let u be the red car's speed and v be the blue car's speed. The distance traveled will equal to speed multiplied by time.
Since both cars met up at point C , their combined speed towards each other could be set up in the equation: 6 0 0 = 6 × ( u + v ) ; u + v = 1 0 0 .
Now, for the rest of the next journey with time t , the red car had traveled 1 6 0 km.:
u t = 1 6 0
This time t was the same time the blue car used to finish up the final distance, which the red car had first traveled. In other words, the first distance = 6 u = v t . Therefore, t = v 6 u .
Substituting this term in the previous equation, we'll get: u t = v 6 u 2 = 1 6 0 .
3 u 2 = 8 0 v = 8 0 ( 1 0 0 − u )
3 u 2 + 8 0 u − 8 0 0 0 = 0
( u − 4 0 ) ( 3 u + 2 0 0 ) = 0
Thus, u = 4 0 ; v = 6 0 ; t = 6 0 6 × 4 0 = 4 .
In other words, in 1 0 hours, the blue car had traveled 6 0 × 1 0 = 6 0 0 km. while the red car had traveled 4 0 × 1 0 = 4 0 0 km. and would have 2 0 0 km. to go.
As a result, it would take 4 0 2 0 0 = 5 hours more for the red car to travel from point D to the destination B .