2 Kites & 1 Triangle Riddle
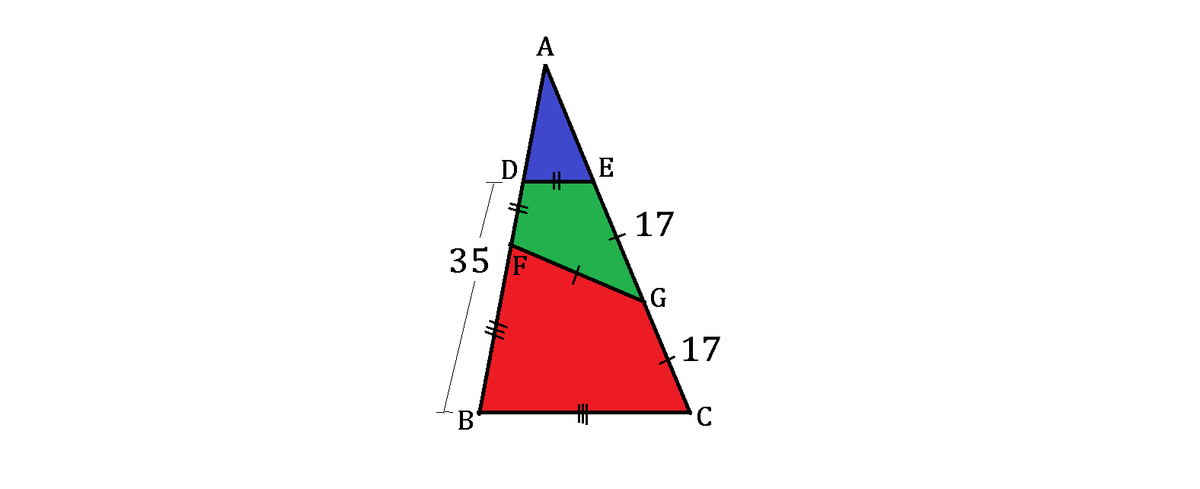
As shown above, a △ A B C is partitioned by 2 segments D E and F G .
D E is parallel to B C , forming a trapezoid B C E D , while F G divides the trapezoid into 2 kites: the red B C G F and the green D E G F . All side lengths between any points with in these kites are whole integers.
G F = G C = G E = 1 7 , and B D = 3 5 .
What is the area of the blue △ A D E ?
Note : Figure not drawn to scale.
The answer is 112.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
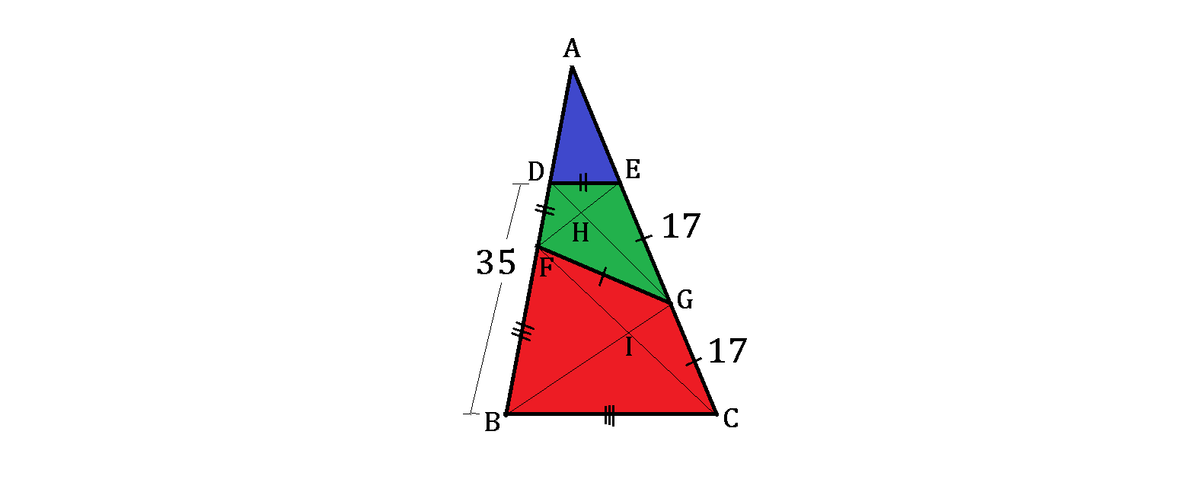
Let us add the diagonals to the kites stated in the question and designate the intersection points as H within the green kite and I within the red one, as shown above.
Since D E ∣ ∣ B C , the triangles A D E and A B C are similar, and so we will attempt to find the ration between B C : D E . Suppose D E B C = k for some constant k . Then the area of A B C is k 2 times that of A D E .
In order to find such ratio, we will determine the desired lengths by investigating the diagonals in both kites. First, the diagonals B G and \GD) both bisect the red and the green kites respectively. Thus, ∠ C G B = ∠ B G F and ∠ F G D = ∠ D G E , and since these four angles add up to a straight angle, 1 8 0 = 2 ∠ B G F + 2 ∠ F G D . Hence, we can prove that 9 0 = ∠ B G F + ∠ F G D = ∠ B G D , the right angle.
Then due to the kite properties, the diagonals within will be perpendicular to each other, making both ∠ F I G and ∠ F H G right angles as well. As a result, F I G H is a rectangle with the diagonal F G = 1 7 , as in the question.
Then let F H = x and F I = y and F D = D E = z . According to Pythagorean theorem, x 2 + y 2 = 1 7 2 . With F I G H as the rectangle, B G ∣ ∣ F E and F C ∣ ∣ D G , and so the triangles B I F and F H D are similar. Also, because, B C = B F and D E = D F , the ratio of B F : F D is also k as well. Here fore, k = z 3 5 − z . Then considering the triangle B I F , ( k x ) 2 + y 2 = ( k z ) 2 , and for F H D , x 2 + ( k y ) 2 = z 2 .
Now we will arrange the system of equations for these variables:
x 2 + y 2 = 1 7 2 ( z x ( 3 5 − z ) ) 2 + y 2 = ( 3 5 − z ) 2 x 2 + ( 3 5 − z y ( z ) ) 2 = z 2
Solving the equations, we will obtain x = 8 ; y = 1 5 ; and z = 1 0 . Then k = 1 0 3 5 − 1 0 = 2 5 , and so B C = B F = 2 5 . Consequently, B I = 2 8 × 5 = 2 0 , and D H = 5 1 5 × 2 = 6 .
Furthermore, the area of the red kite B C G F = 2 1 × 2 × 1 5 × ( 2 0 + 8 ) = 4 2 0 .
The area of the green kite D E G F = 2 1 × 2 × 8 × ( 1 5 + 6 ) = 1 6 8 .
Then let S be the solution area of the triangle A D E . We can write k 2 S = S + 1 6 8 + 4 2 0 = S + 5 8 8 .
Thus, ( k 2 − 1 ) S = 5 8 8 = ( 4 2 5 − 4 ) S = ( 4 2 1 ) S .
Finally, S = 2 1 4 × 5 8 8 = 1 1 2 .
Draw diagonals D G and E F intersecting at H , diagonals C F and B G intersecting at I , and a circle centered at G with a radius of 1 7 passing through C , E , and F .
Since C E is a diameter of the circle, by Thales' Theorem ∠ C F E = 9 0 ° . Since all side lengths between any points within the kites are whole integers, E F and C F are integers; therefore, the sides of △ C E F are a Pythagorean triple with a hypotenuse of 3 4 , which could only be ( 1 6 , 3 0 , 3 4 ) . Therefore, E F = 1 6 and C F = 3 0 .
By properties of diagonals of kites, ∠ F I B = 9 0 ° and F I = C I ; and since C F = 3 0 , F I = C I = 1 5 . Similarly, ∠ D H F = 9 0 ° and F H = H E = 8 .
△ D H F and △ F I B are similar by AA similarity, so B F D F = F I D H . If x = D F , then B F = 3 5 − x and by Pythagorean's Theorem on △ D H F , D H = x 2 − 8 2 . Now the similarity ratio is 3 5 − x x = 1 5 x 2 − 8 2 , which has one integer solution of x = 1 0 .
Using Pythagorean's Theorem and the similarity ratio, D E = 1 0 , D H = 6 , H G = 1 5 , G I = 8 , B I = 2 0 , and B F = B C = 2 5 ; and combining the area of each right triangle gives trapezoid B C E D an area of A B C E D = 5 8 8 .
△ A D E and △ A B C are similar by AA similarity, and has an area ratio of B C 2 D E 2 = 2 5 2 1 0 2 = 2 5 4 . If A △ A D E is the area of △ A D E , then 2 5 4 = A △ A D E + 5 8 8 A △ A D E , which solves to A △ A D E = 1 1 2 .