2 odd polygons inside a even polygon

Geometry Level 3

This is the corrected version of my previous problem. All the polygons in the image are regular. Now if you see the pattern,

1st figure, There is an octagon inside which there is a pentagon and a triangle inscribed. And you can see that the pentagon and triangle are constructed on a pair of parallel sides of the octagon. And also $8 = 5 +3.$

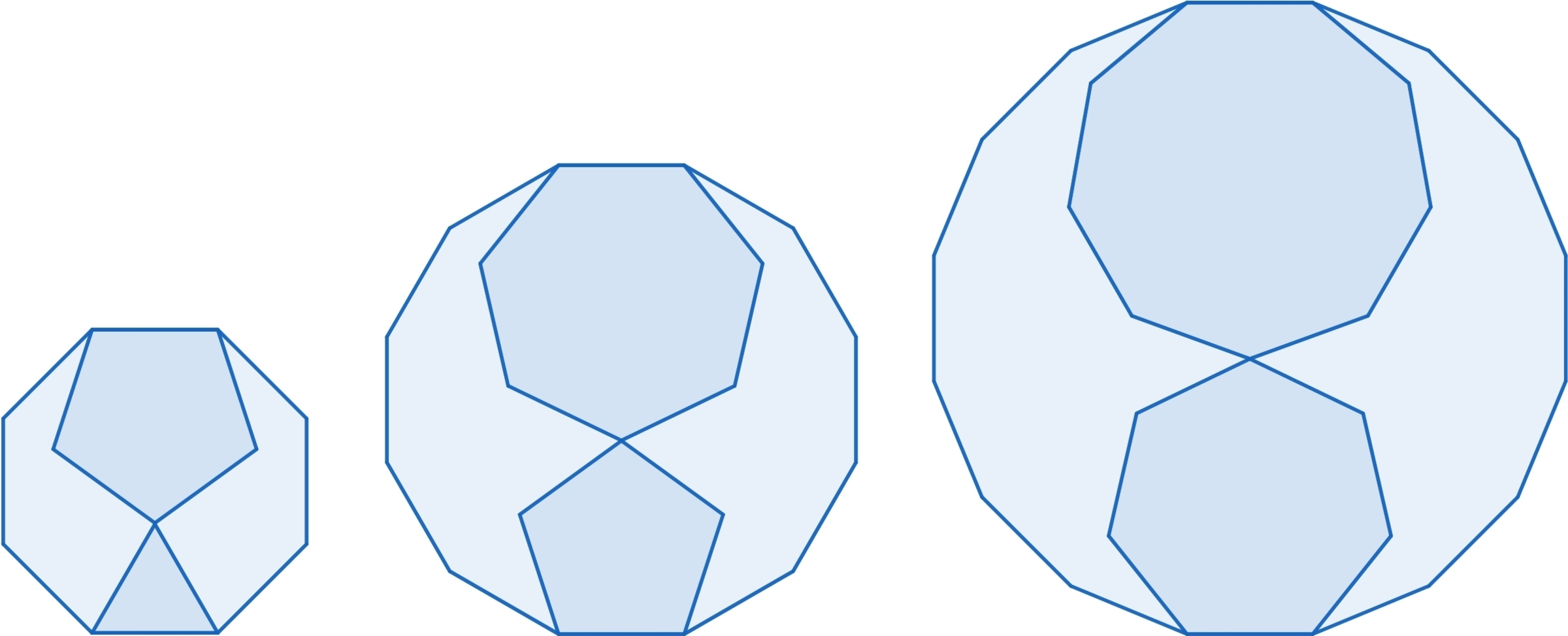
One of the vertices of pentagon and triangle seem to coincide but rather that is a illusion (thanks to Chris Lewis) actually there is a gap between the pentagon and triangle. A similar statement can be made for other 2 figures.

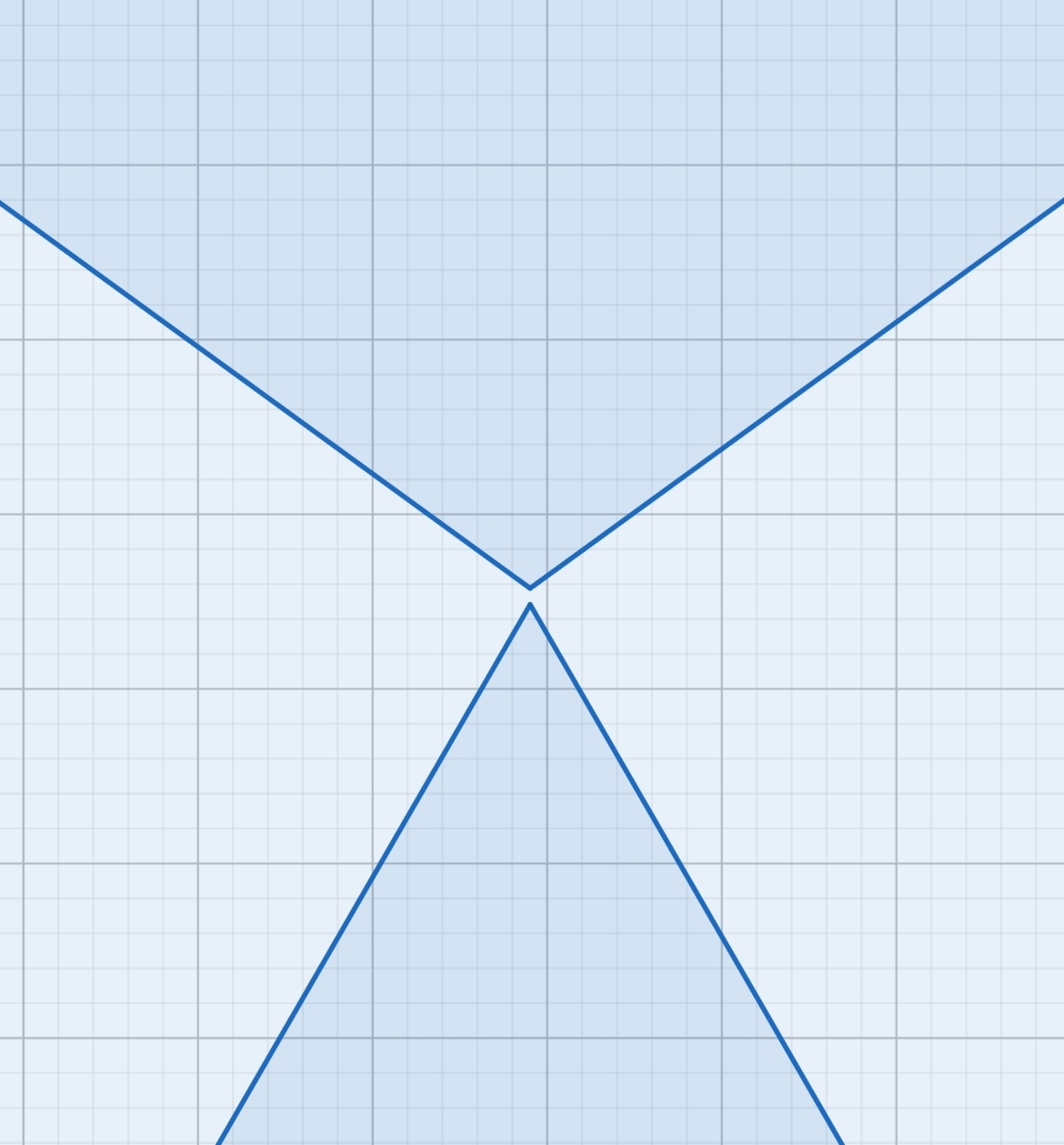This is zoomed version of the pentagon and triangle

Now my question, if this pattern continues will the gap between the 2 odd sided polygon ( inscribed in a $4n$ -sided polygon where n $\geqslant$ 2 ) ever become 0?

Yes No

2 solutions

Omek K
Apr 6, 2021

I am not sure of this solution but just check it.

First the polygon's general composition is 4n sided polygon, 2n+1 and 2n-1 sided polygons and let all of them be unit polygons.

Let us define the height of a 2n-1 sided polygon as function g(n). So in the figure there is pentagon but a similar figure would be there for a 2n-1 sided polygon.

As one see Q is the center of the circumcircle. And all the triangles are congruent. Therefore,

the required height of the polygon
= height of one triangle + radius of the circumcircle
= height of triangle + one of equal sides of the triangle

$\begin{aligned} \therefore g(n) &= QU + QT\\ &= UR ×tan(\angle QRU) + UR ×sec(\angle QRU)\\ &= UR (tan(\frac{\angle SRU}{2}) + sec(\frac{\angle SRU}{2}))\\ &= UR (tan(\frac{(2n-3)\pi}{2(2n-1)}) + sec(\frac{(2n-3)\pi}{2(2n-1)}))\\ &= 0.5 (tan(\frac{(2n-3)\pi}{4n-2}) + sec(\frac{(2n-3)\pi}{4n-2})) \end{aligned}$

Now for the length between a pair of $\parallel$ sides. Let us define f(n) as this length for 4n sided polygon.

Draw a similar image for the 4n sided polygon. It is easy to see that if one joins the opposite ends of the parallel sides we get the longest diagonal and it is a line of symmetry. Therefore it bisects the $\angle SLM$ .

$\begin{aligned} \therefore f(n) &= PM\\ &= LM ×tan(\angle PLM)\\ &= LM ×tan(\frac{\angle SLM}{2})\\ &= LM ×tan(\frac{(4n-2)\pi}{2(4n)})\\ &= 1 ×tan(\frac{(2n-1)\pi}{4n})\\ &= tan(\frac{(2n-1)\pi}{4n}) \end{aligned}$

Let us now define h(n) as gap between the polygons. $\therefore$ h(n) = f(n) - ( g(n) + g(n+1) ) where n $\geqslant$ 2. And this h(n) is decreasing function. Therefore some huge value of n will make this function approach zero, thereby making the gap between interior polygons zero.

Doug Brunson
Apr 7, 2021

In the limit as the polygon sides approaches infinity, we will have a exterior circle with two equal-sized circles inside. These two circles must touch each other. Consider Omek's solution, he derives a decreasing function, which has a limit of zero. But, does his gap function actually have a root, N?

2 odd polygons inside a even polygon

2 solutions

0 pending reports