2 squares
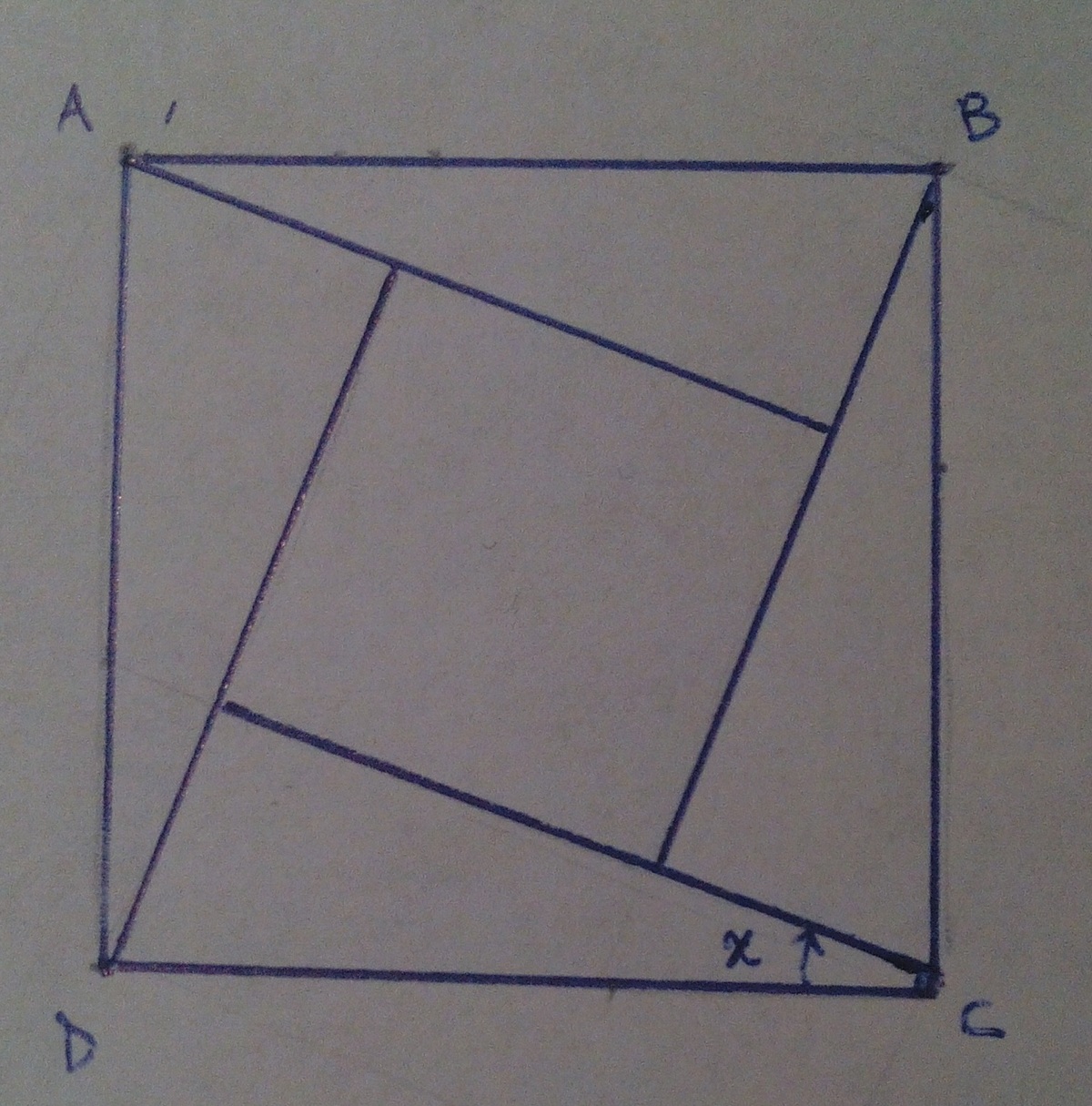
Let A B C D be a square. The area of the blue square is 2 1 of the area of A B C D .
Find the angle x in degrees.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Let a be the side of the big square. There are total 4 congruent wedges of brown color. Let the smaller side of the wedge be x & y be the larger side, so that tan X = y x Now, applying Pythagoras to one of the wedge, x 2 + y 2 = a 2 … ( 1 )
Since the area of blue square is half the area of big square that means the sum of areas of the four wedges is also half the area of big square . ⇒ 4 • 2 x y = 2 a 2
⇒ x y = 4 a 2 . . . ( 2 )
Dividing ( 1 ) by ( 2 ) we get, y x + x y = 4 Further solving this gives y x = tan X = 2 ± 3 Dropping the larger value, tan X = 2 − 3 ⇒ X = 1 5 °
this is construction of bhaskara's proof of pythagoras!
It is to solve cos(x) - sin(x) = 1/sqrt(2). Squaring this, we get sin(2x) = 1/2, i.e. x = 15(deg)
i don't understand how "cos(x) - sin(x) = 1/sqrt(2)"? can anyone explain?
Log in to reply
Let, 'a' be the side of larger square.
The triangles are all congruent. So, Side ( Smaller Square ) = Larger Side of Triangle - Smaller Side of Triangle or, Side ( Smaller Square ) = a cosx - a sinx or, a/ sqrt(2) = a ( cosx - sinx ) or, cosx - sinx = 1/ sqrt(2).
May you please explain how did you arrive at it?
Beautiful!
HOW BY SOLVING FURTHER COS(X)-SIN(X) WE GET X =15
Let M be the midpoint of A B , O the common center of both squares and P the vertex of the blue square such that ∠ A P B is right angled. Let a be the side length of the original square.
As A B C D is a square and M is the circumcenter of △ A P B , we have O M = 2 a = M B = M P . Also, as the blue square's area is one half of the original square's area, its diagonal is equal to 2 1 times the original square's diagonal. By the Pythagorean theorem, the original diagonal has length equal to a 2 and hence the diagonal of the blue square measures a . Then, as O P is half of the diagonal, 2 a = O P = O M = M P and hence △ O P M is equilateral and ∠ O M P = 6 0 ∘ .
Now:
∠ A M P = ∠ A M O + ∠ P M O = 9 0 ∘ + 6 0 ∘ = 1 5 0 ∘
And since M P = M A , this imples ∠ M A P = 1 5 ∘ , which is the desired angle.
Well done Ariel! Maybe you should explain why O is common center of both squares.
Side of the small square = p units. Smallest side of the 4 given right triangles = y units. (p+y)^2 + y^2 = 2 * p^2 => (1+ y/p)^2 + (y/p)^2 =2 => 2 (y/p)^2 + 2 (y/p) -1=0 => (y/p) = {-1 +- root(3) }/2 Thus y/(y+p) = {root(3)-1}/{1+root(3)} Thus tan (x) = {tan A - tan B }/ {1+tanA*tanB} = tan (A-B) tan 45 =1 , tan 60 = root(3) Thus y/y+p = tan (60 -45) = tan 15 Thus x= 15.
4 ar(triangle) + ar(blue square) = ar(ABCD) => ar(triangle) = 1/8 * ar(ABCD) = a^2 /8 or, 1/2 * a^2 * sinx cosx = a^2 /8 or, sinx*cosx = 1/4 => sin2x = 1/2 => x = 15 degrees
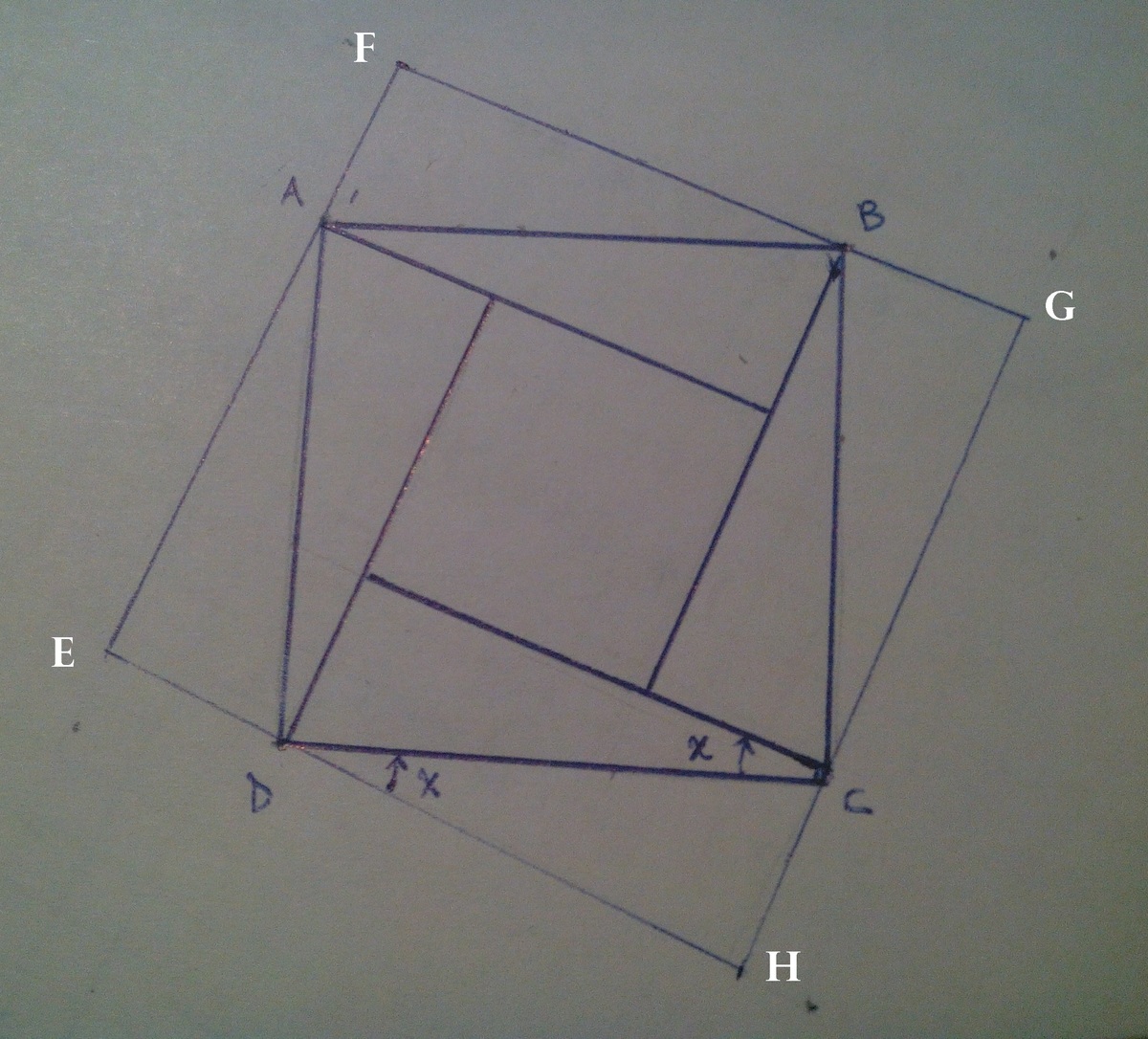
From the second draw we can see that the area of the internal square is
3
1
of the area of EFGH because we have duplicated the triangles.
If
l
is the side of ABCD we can say that
D
H
ˉ
=
l
⋅
c
o
s
x
and
E
D
ˉ
=
l
⋅
s
i
n
x
. So
3
[
l
⋅
(
s
i
n
x
+
c
o
s
x
)
]
2
=
2
l
2
→
s
i
n
2
x
+
c
o
s
2
x
+
2
s
i
n
x
c
o
s
x
=
2
3
→
s
i
n
2
x
+
c
o
s
2
x
+
2
s
i
n
x
c
o
s
x
=
2
3
→
s
i
n
2
x
=
2
1
→
x
=
1
5
o
cos(x) - sin(x) = 1/sqrt(2). Squaring Both sides sin^2(x)+cos^2(x)+2sin(x)cos(x)=1/2 1+sin(2x) = 1/2, sin(2x)=-1/2 After Taking inverse x = 15(deg)
Let L be the side of the brown square and l the side of the blue square. Then l=L cos(x)-Lsin(x)=L (cos(x)-sin(x)) As l^2/L^2=1/2 (areas) we get (cos(x)-sin(x))^2=1/2 or 1 -sin(2x)=1/2 From here 2x=30º or x=15º
let the side of ABCD be y ............... area of ABCD = y^2........... let the inner square be named PQRS .........area of inner square = y^2/2........ side of inner square PQRS = y/sqrt(2)...... let us assume the side of ABCD as sqrt(2) , then the side of PQRS = 1...... let BQ = x..... then applying pythagoras theorem for ABQ, AB^2 = BQ^2 + AQ^2....... we get x = [sqrt(3)-1]/2....... so sinX = BQ/AB....... X = sin inverse of BQ/AB..... we get X = 15.07 degrees or 15 degrees.
let BC= a , perpendicular and base of triangle(in brown color) will be 'aSinx' and 'aCosx' ..area of triangle = 1/2 a^2 SinxCosx ..4 X area of triangle = area of inner square = area of ABCD/2 ==> 4 Sinx Cosx = 1 ==> Sin2x=1/2 ==> 2X=30 ==>X=15
let the side of the larger square be a.. so its area is a^2..so,sum of the area of the four triangles is a^2-(a^2/2)=a^2/2.. as all the triangles are congruent,so area of each is (a^2/2)/4=a^2/8... now this area is 1/2 asin(x) acos(x)=1/4 a^2 sin(2x)... so, sin(2x)=1/2=>2x=30 deg so, x=15 deg
well done dear
Let j=side length of blue square, let k=side length of red square. k^2=2 j^2. Also the total area of the four red triangles is k^2-j^2 =j^2. The area of one triangle is (1/2) (k cos(x)) (k sin(x))=(1/2) k^2 cos(x) sin(x)=j^2 cos(x) sin(x). The total area of the four triangles is j^2=4 j^2 cos(x) sin(x) or cos(x) sin(x)=1/4. The solution is x=15 or 75 degrees which are complementary angles. Since x is illustrated as the smaller angle in the figure, therefore x=15 degrees.
Let the side of the LARGER square = a .
Since the four right triangles are congruent,
the LONGER leg of the triangle = a cos x°
while the SHORTER leg of the triangle = a sin x° .
So it would follow that the
side of the SMALLER square = a cos x° - a sin x° .
Therefore,
Area of LARGER square = a ² .
Area of SMALLER square = ( a cos x° - a sin x° ) ² .
Given that the area of the SMALLER square is 1/2 of the area of the LARGER square, we have this ;
a ² / 2 = ( a cos x° - a sin x° ) ²
a / √2 = ( a cos x° - a sin x° )
a / √2 = a ( cos x° - sin x° )
1 / √2 = cos x° - sin x°
½ = cos ² x° - 2 cos x° sin x° + sin ² x
½ = cos ² x° + sin ² x° - 2 cos x° sin x°
Pythagorean identity states that; cos ² x° + sin ² x° = 1
½ = 1 - 2 cos x° sin x°
2 cos x° sin x° = 1 - ½
2 cos x° sin x° = ½
Double angle identity states that; sin ( 2 x ) = 2 cos x° sin x°
sin ( 2 x ) = ½
2 x = 30°
x = 15°