Two Tangent Lines
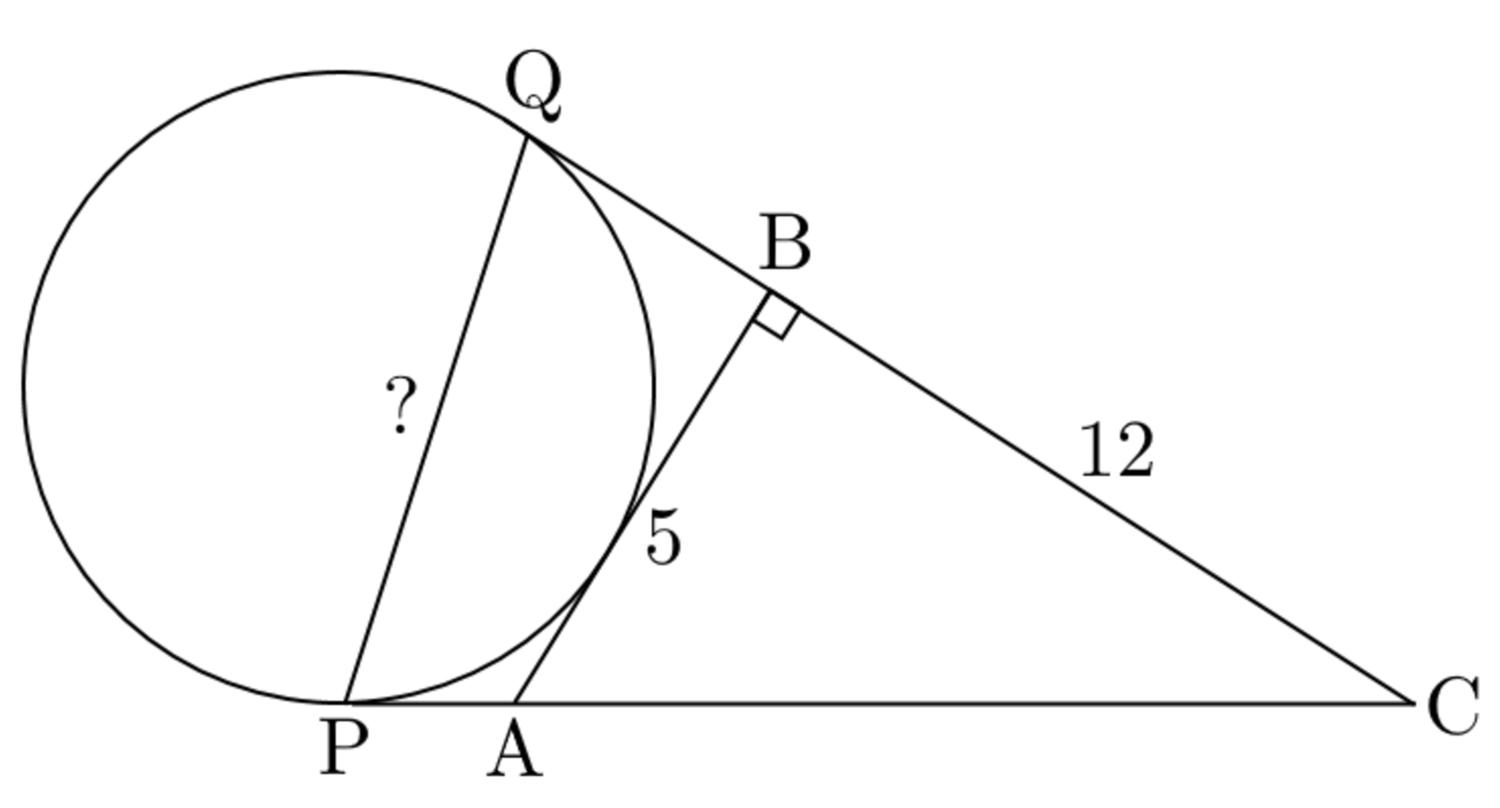
A B C is a right triangle with ∠ B = 9 0 ∘ , A B = 5 , B C = 1 2 , and A B tangent to a circle. C P and C Q are also tangent to the circle at P and Q respectively.
If the length of chord P Q is c a b , where a , b , and c are positive integers, with a and c being coprime and b square-free, find a + b + c .
The answer is 54.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
nice approach!
First, A C ˉ = 5 2 + 1 2 2 = 1 3 .
△ C P Q is an isosceles triangle and A B ˉ is another tangent line, so we get 2 equations.
{ A P ˉ + A C ˉ = B Q ˉ + B C ˉ A P ˉ + B Q ˉ = A B ˉ
→ { A P ˉ + 1 3 = B Q ˉ + 1 2 → B Q ˉ = A P ˉ + 1 A P ˉ + B Q ˉ = 5
→ { A P ˉ = 2 B Q ˉ = 3
According to Cosine Rule, we get
c o s A C B = 1 3 1 2 = 2 × 1 5 × 1 5 1 5 2 + 1 5 2 − P Q ˉ 2
Therefore, P Q ˉ = 1 3 4 5 0 = 1 3 1 5 2 6
So the final answer is 1 5 + 2 6 + 1 3 = 5 4 .
You should mention in the problem that a and c are coprime and b is square free.
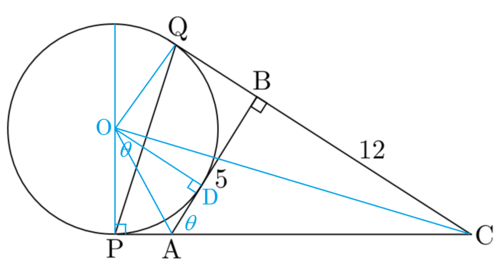
Let the center of the circle be O and its radius r . Then we note that O P C is a right triangle with ∠ O C P = 2 1 ∠ C . Since tan C = 1 2 5 ⟹ tan ∠ O C P = 5 1 . Now C P = O P cot ∠ O C P = 5 r .
Let A B be tangent to the circle at D . Then O D is perpendicular to A B and is parallel to CQ. Hence ∠ D O P = ∠ A = θ . Since △ A O D and △ A O P are congruent, ∠ A O D = ∠ A O P = 2 θ . Then we have:
tan ∠ A O P tan 2 θ 3 2 ⟹ r = O P A P = O P C P − A C = r 5 r − 1 3 = r 5 r − 1 3 = 3 By Pythagorean theorem A C = 1 3 Since tan θ = 5 1 2 ⟹ tan 2 θ = 3 2
Therefore C P = C Q = 5 r = 1 5 and P Q = 2 C P sin 2 C = 2 6 3 0 = 1 3 1 5 2 6 . Hence a + b + c = 1 5 + 2 6 + 1 3 = 5 4 .
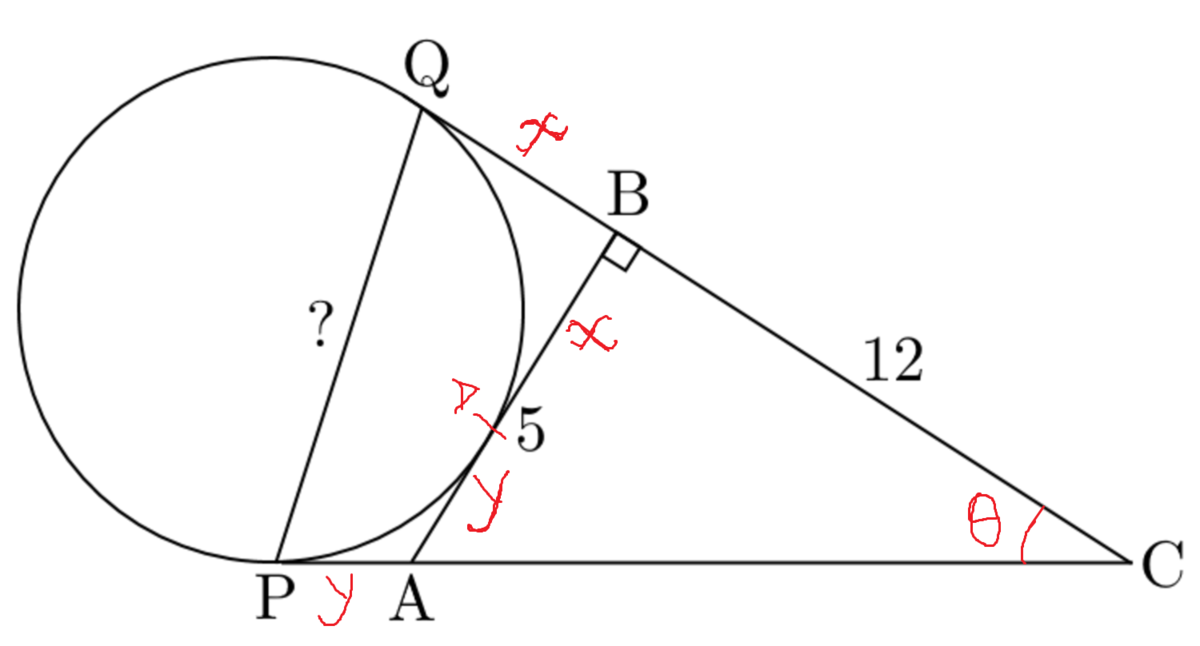
AC = 13 by Pythagoras Theorem in triangle ABC
as they are tangents then BQ=BD and AP=AD let BQ=BD=x and AP=AD=y
also CQ = CP (they are also tangents from a single point)
from the figure we see x+y = 5
and 12+x = 13+y (CQ=CP) this gives us : x-y = 1
so , x+y= 5 and x-y=1
from here we get x=3 and y = 2
hence , CQ=CP=15
now again in Triangle ABC cos Θ = 1 3 1 2
And in Triangle PQC we apply cosine formula
so, cos Θ = 2 ∗ 1 5 ∗ 1 5 2 2 5 + 2 2 5 − P Q 2 = 1 3 1 2
now we can solve and find PQ
Radius of circle can be shown equal to 3, QC =PC=15 and PQ=30/(26)^0.5
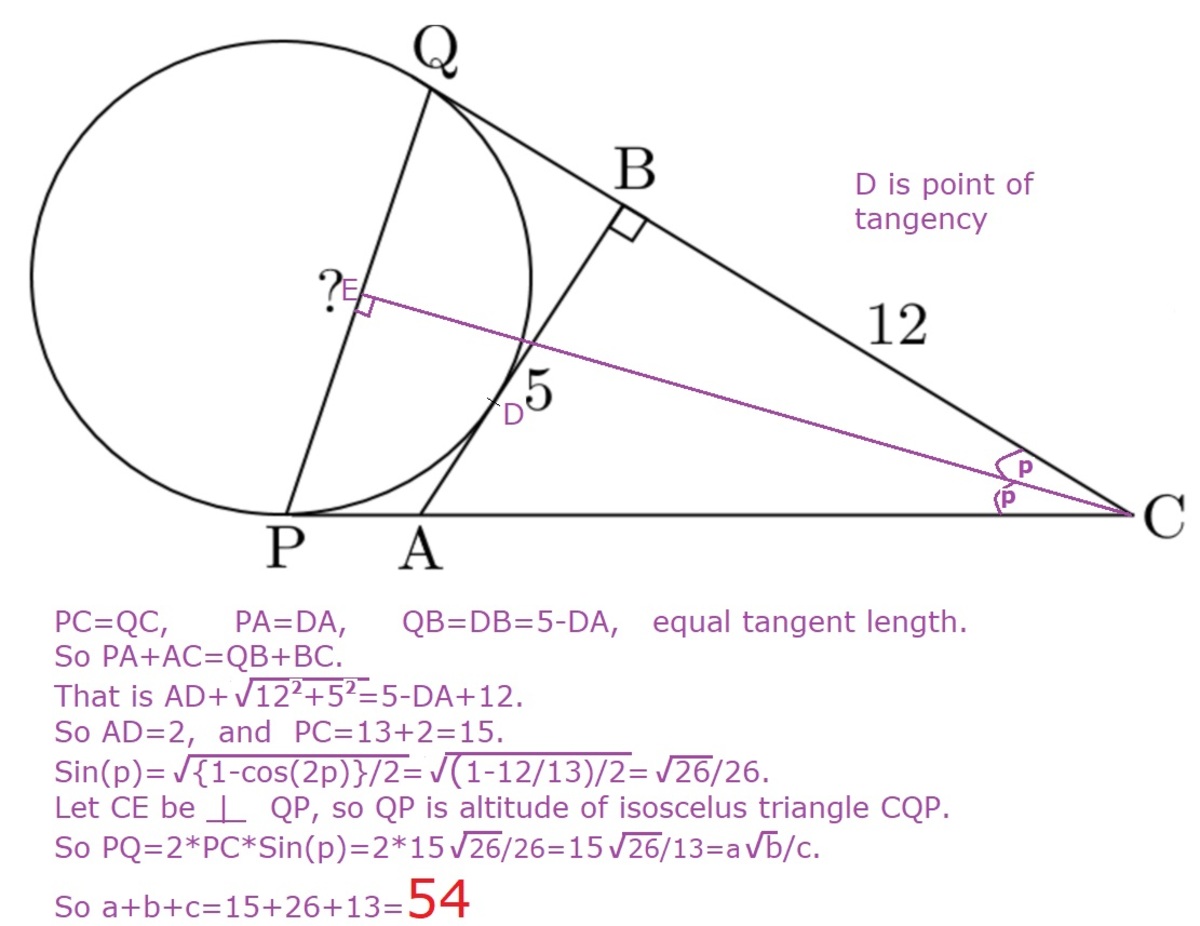
Since A C = 1 3 (By Pythagorean theorem) , let A P = x , therefore P C = x + 1 3 = Q C = Q B + 1 2 which implies Q B = x + 1 .
Now let the point of contact of A B with the circle be equal to O . Now we know that A P = A O = x and B Q = B O = x + 1 , which implies x + x + 1 = 5 ⟹ x = 2 = A P . Therefore B Q = 3 .
Now draw a parallel line through A to P Q to cut C Q at D . Now we can see that A D Q P is an isosceles trapezium as ∠ C Q P = ∠ C P Q . This implies A P = D Q = 2 . So B D = 1 . Now again by Pythagorean theorem, we have A D = 1 2 + 5 2 = 2 6 .
Since △ C Q P is similar to △ C D A , we have P Q A D = C Q C D (because sides of similar triangles are proportional) ⟹ P Q 2 6 = 1 5 1 3 . Therefore P Q = 1 3 1 5 2 6 making the answer 5 4 .