Octagon in an Octagon
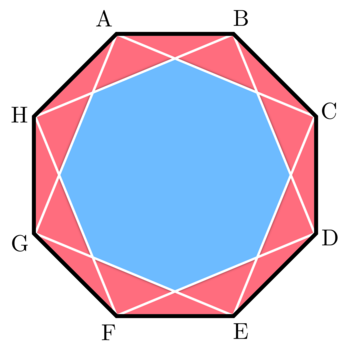 A regular octagon
A
B
C
D
E
F
G
H
has squares
A
C
E
G
and
B
D
F
H
inscribed in it. These squares form a smaller octagon as shown.
A regular octagon
A
B
C
D
E
F
G
H
has squares
A
C
E
G
and
B
D
F
H
inscribed in it. These squares form a smaller octagon as shown.
Let the the area of octagon A B C D E F G H be A L and the area of the smaller octagon be A S . Then for some integers a and b , where b is square-free, A L A S = a − b . Find a + b .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Same method! :)
One can easily prove that the ratio of side of smaller octagon to that of larger octagon is
= 2 cos 8 π 1
we know that the ratio of areas of similar regular polygons is equal to the ratio of squares of their respective sides hence
A L A S = ( 2 cos 8 π 1 ) 2 = 2 sec 2 8 π = 2 1 + tan 2 8 π = 2 1 + ( 2 − 1 ) 2 = 2 4 − 2 2 = 2 − 2
Let x the side of larger octagon, the square side y, y^2 = x^2(2 +√2), Let z the side of smaller octagon, (1+√2)z = y, z^2 = y^2/(3 +2√2), By similarity AS/AL= z^2 / x^2 = (2 +√2)/ (3 +2√2) = 2 - √2 = a - √b, a+b=4
Let the side length of octagon A B C D E F G H be x . Then A L = 2 x 2 ( 1 + 2 ) .
Consider △ A B H : Let the length of line B H be y - this is the length of a side of the squares A C E G and B D F H . Using the cosine rule, we have y 2 = x 2 + x 2 − 2 x 2 cos 1 3 5 ° ⇒ y 2 = 2 x 2 ( 1 + 2 / 2 ) .
Now let the side length of the smaller octagon be z . Then z ( 1 + 2 ) = y and A S = 2 z 2 ( 1 + 2 ) .
⇒ A L A S = 2 x 2 ( 1 + 2 ) 2 z 2 ( 1 + 2 ) = x 2 z 2 = x 2 ( 1 + 2 ) 2 y 2 = x 2 ( 1 + 2 ) 2 2 x 2 ( 1 + 2 / 2 ) = ( 1 + 2 ) 2 2 ( 1 + 2 / 2 ) = 3 + 2 2 2 + 2 = 2 − 2
Thus a = b = 2 , and the required answer is 4 .