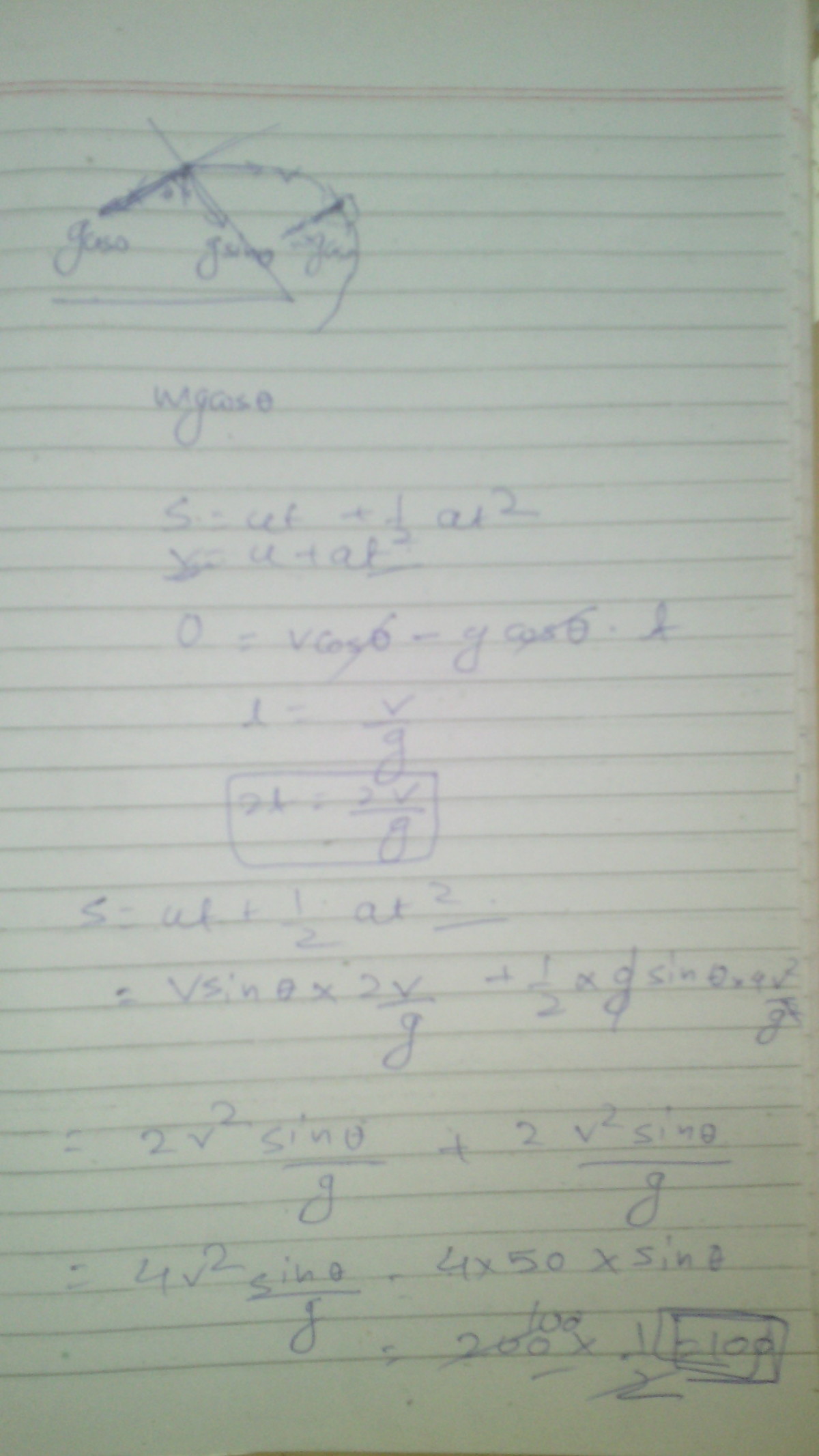200 followers problem
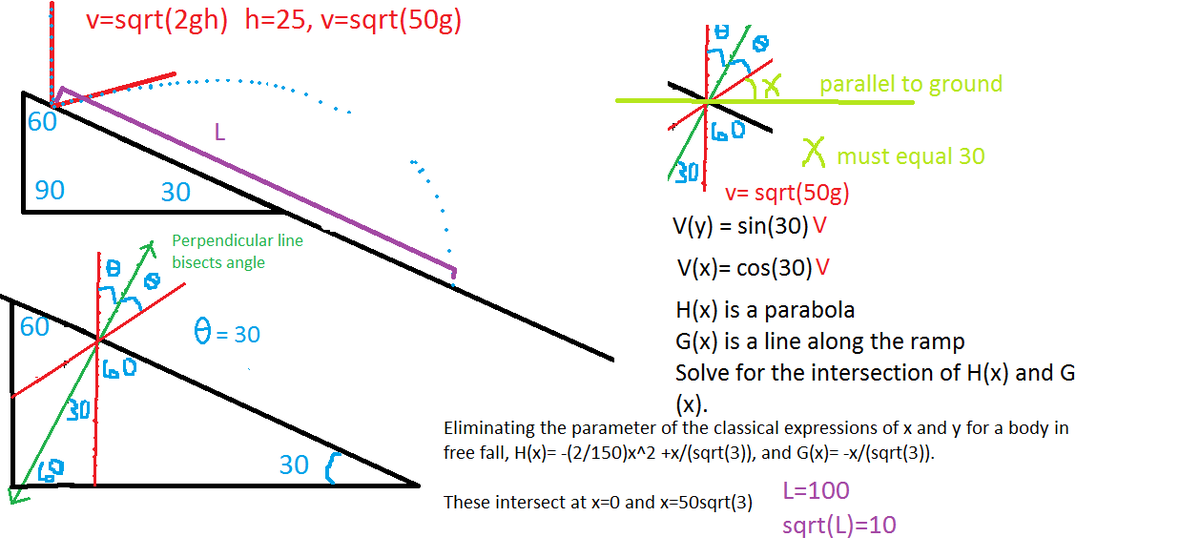
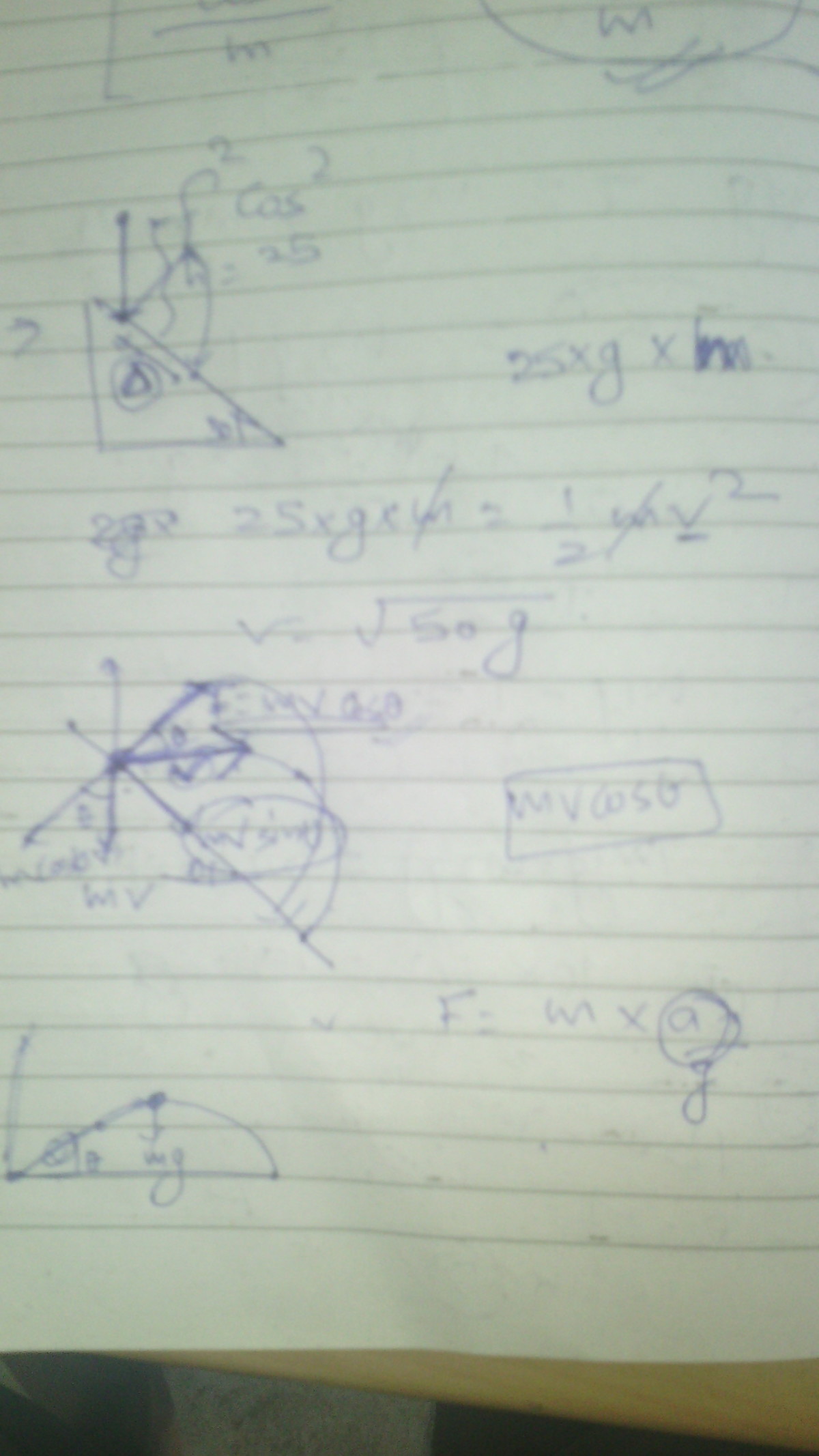
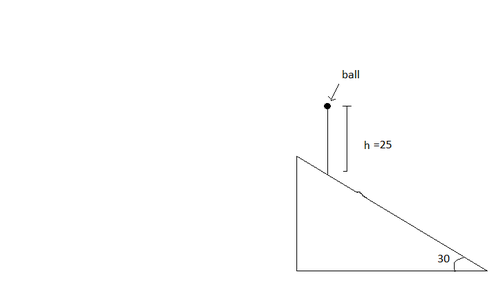 If distance between the two points on the fixed
smooth
inclined plane on which the ball makes first and second collision can be represented as
.
If distance between the two points on the fixed
smooth
inclined plane on which the ball makes first and second collision can be represented as
.
Find .
Details
- Collisions are perfectly elastic. -surface of inclined plane is smooth.
- No air resistance.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.