200 Followers Question by Dr. Warm
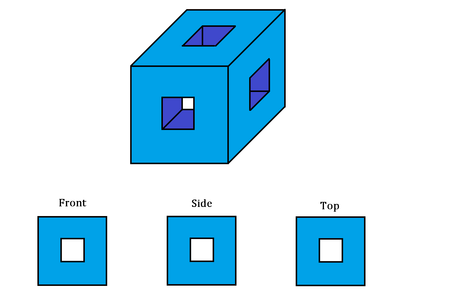
A cube is drilled along the vertical, horizontal, and ventral axes such that a square hole can be seen in all front, side, and top views, as shown above.
What is the total surface area of this structure in ?
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The surface area of the outer surface is ( 3 2 − 1 2 ) ( 6 ) = ( 8 ) ( 6 ) = 4 8 c m 2 .
The surface area of the inner surface is ( 1 2 ) ( 4 ) ( 6 ) = 2 4 c m 2 .
The total surface area of the structure is 4 8 + 2 4 = 7 2 c m 2
answer: 7 2 c m 2