2015 Countdown Problem 12: Sums of consecutive numbers
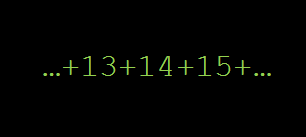How many integers between 2 and 2015 inclusive cannot be expressed as a sum of at least two consecutive positive integers?
This problem is part of the set 2015 Countdown Problems .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
True that, will amend accordingly. Thanks! :)
To add two or more consecutive numbers at least one has to be odd. Any power of 2 can not be built by summation that include an odd number. A n y o d d n u m b e r > 1 , can always be obtained by adding the following two consecutive numbers., 2 T h e o d d n u m b e r − 1 + 2 T h e o d d n u m b e r + 1 . A n y e v e n n u m b e r may be obtain by adding only odd number of consecutive numbers, if the middle term is even. This middle term is also the average. So the sum would be number of terms (which is odd) * (middle term) = 2 a n i n t e g e r
2 (power) number's are only not consecutive : 2
4
8
16
32
64
128
256
512
1024
2048
4096 etc.
I don,t know why 2 (power) number's are not consecutive. But this is true.
From 2 to 2015 range our answer is 10.
answer = 10.
Moderator note:
This solution has been marked incomplete. You did not explain your reasoning.
Why is it that only numbers of form 2 n are not expressive as sum of consecutive integers ?
In response with respect to Challenge Master : Have you any explain that this solution is incorrect ?
Log in to reply
Shohag....look at Niranjan's solution... he was successful in explaining why only 2^n is a number that cant be represented as the sum of consecutive integers.
But 6 also cannot be expressed in that way
[2]
4
8
16
32
64
128
256
512
1024
[2015]
2048
Based on the intervals from 2 to 2015, or [2,2015], there are only 10 numbers.
Moderator note:
This solution has been marked incomplete. You did not explain your reasoning.
In response with respect to Challenge Master : Have you any explain that this solution is incorrect ?
I have also same concept
The problem should really say "consecutive positive integers". Otherwise the answer would be 0, since ∑ k = − n n + 1 k = n + 1 for any natural number n .