2015 Countdown Problem #15: Palindrome Integration

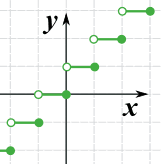Let $x$ be a real number and $f(x)$ be a real-valued function on $x$ such that $f(x)$ is:

• the next palindrome larger than $x$ (if $x$ is not a palindrome); or

• $x$ (if $x$ is a palindrome).

For example, $f(1001)=1001$ , $f(1001.01)=f(1002)=1111$ .

Let

$A=\int _{ 999 }^{ 2015 }{ f(x) \mbox{ } dx }$

$B=f(...(f(f(1603)-58)-58)...)-58$

Find the value of $\frac{A}{B}$ .

This problem is part of the set 2015 Countdown Problems .