2015 Countdown Problem #16: Some Brute Force & Luck Needed – Part I
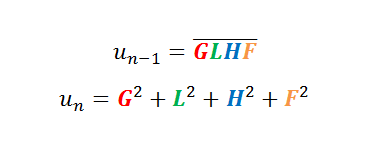 A sequence is defined by the recurrence relation
and
equals the sum of the squares of each digit in
for
.
A sequence is defined by the recurrence relation
and
equals the sum of the squares of each digit in
for
.
How many more square numbers than prime numbers are there between and inclusive?
#GoodLuckHaveFun
This problem is part of the set 2015 Countdown Problems .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The sequence is 2015, 30, 9, 81, 65, 61, (37, 58, 89, 145, 42, 20, 4, 16) and loops back to 37. The first part (unlooped) of the sequence has 2 squares and 1 prime and the looped portion has 2 square and 2 primes. By repeating that loop, the 2015th number in the sequence is 37 (which is a prime). Without calculation, There is one more square than prime in the unlooped portion, no changes after the completed loops and one more prime than square in the unfinished loop leaving a total of zero.