2015 Countdown Problem #18: A Vicious Circle
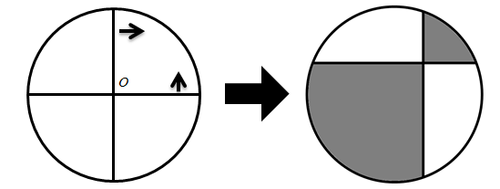 A circle of diameter 2015 cm has one vertical and one horizontal line, both initially intersecting at the centre of the circle.
A circle of diameter 2015 cm has one vertical and one horizontal line, both initially intersecting at the centre of the circle.
The horizontal line is shifted upwards by 20 cm and the vertical line is shifted rightwards by 15 cm.
For each subsequent time, the horizontal line is shifted upwards by the previous distance it shifted, and the vertical line is shifted rightwards by the previous distance it shifted. This process repeats indefinitely.
The end result is shown in the image. Find the difference between the shaded and unshaded areas.
This problem is part of the set 2015 Countdown Problems .
The answer is 2700.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we draw a circle.
Then draw the vertical and horizontal lines.
We now draw the shifted lines where the dashed lines are their original places.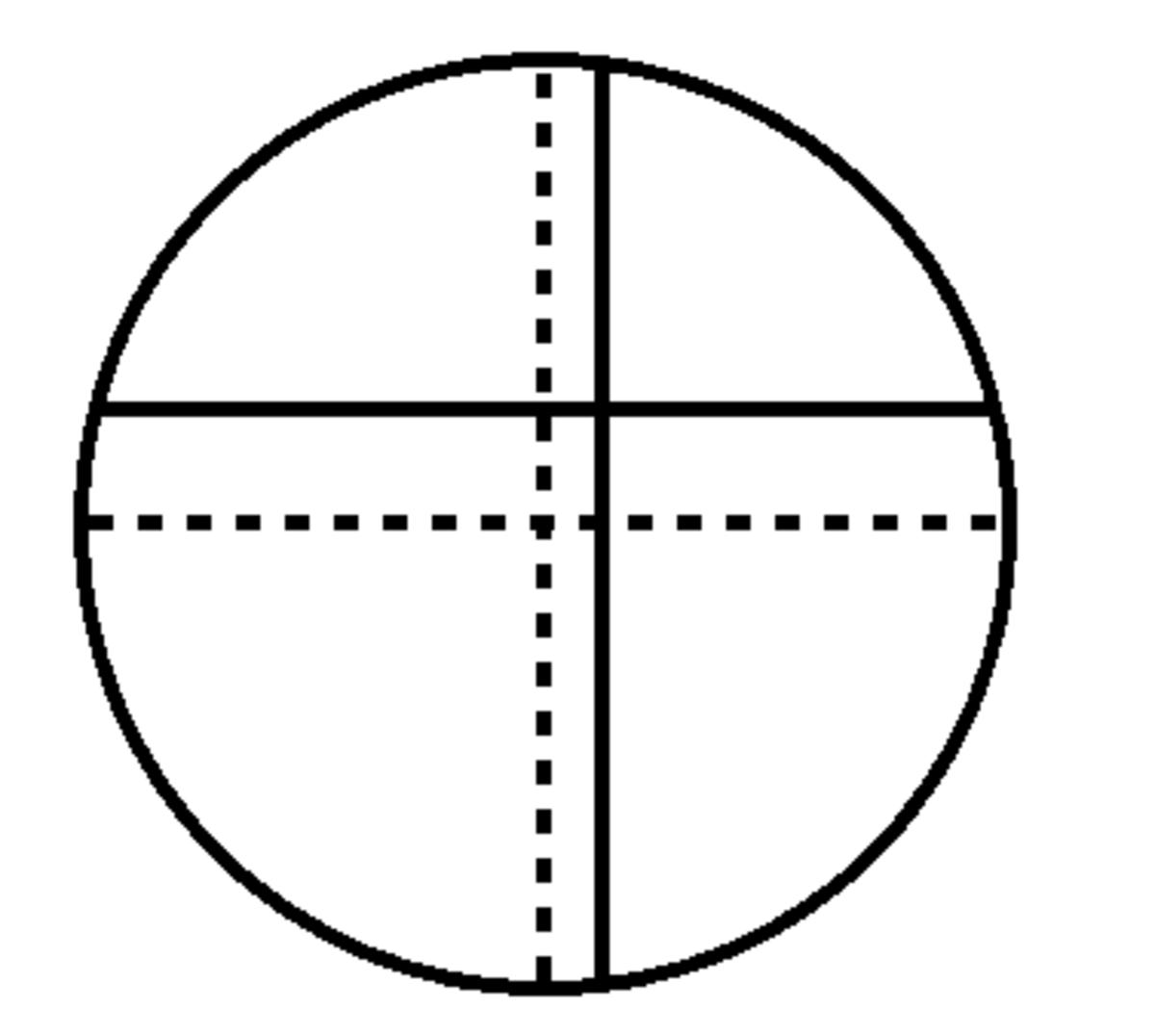
We need to know where they will eventually end.
Since m → ∞ lim n = 0 ∑ m x n 1 = x − 1 x
then m → ∞ lim n = 0 ∑ m 3 n 1 = 2 3
The horizontal line will end 3 0 cm above of the center while the vertical line will end 2 2 . 5 cm to the right of the center.
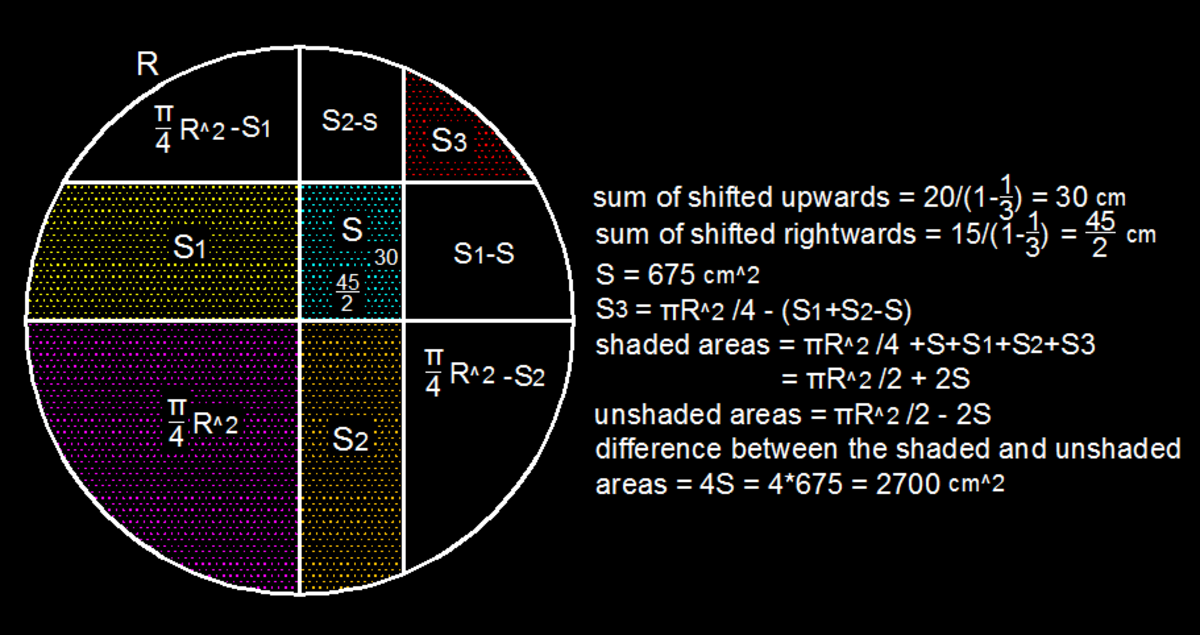
We now label the sections of the previous figure.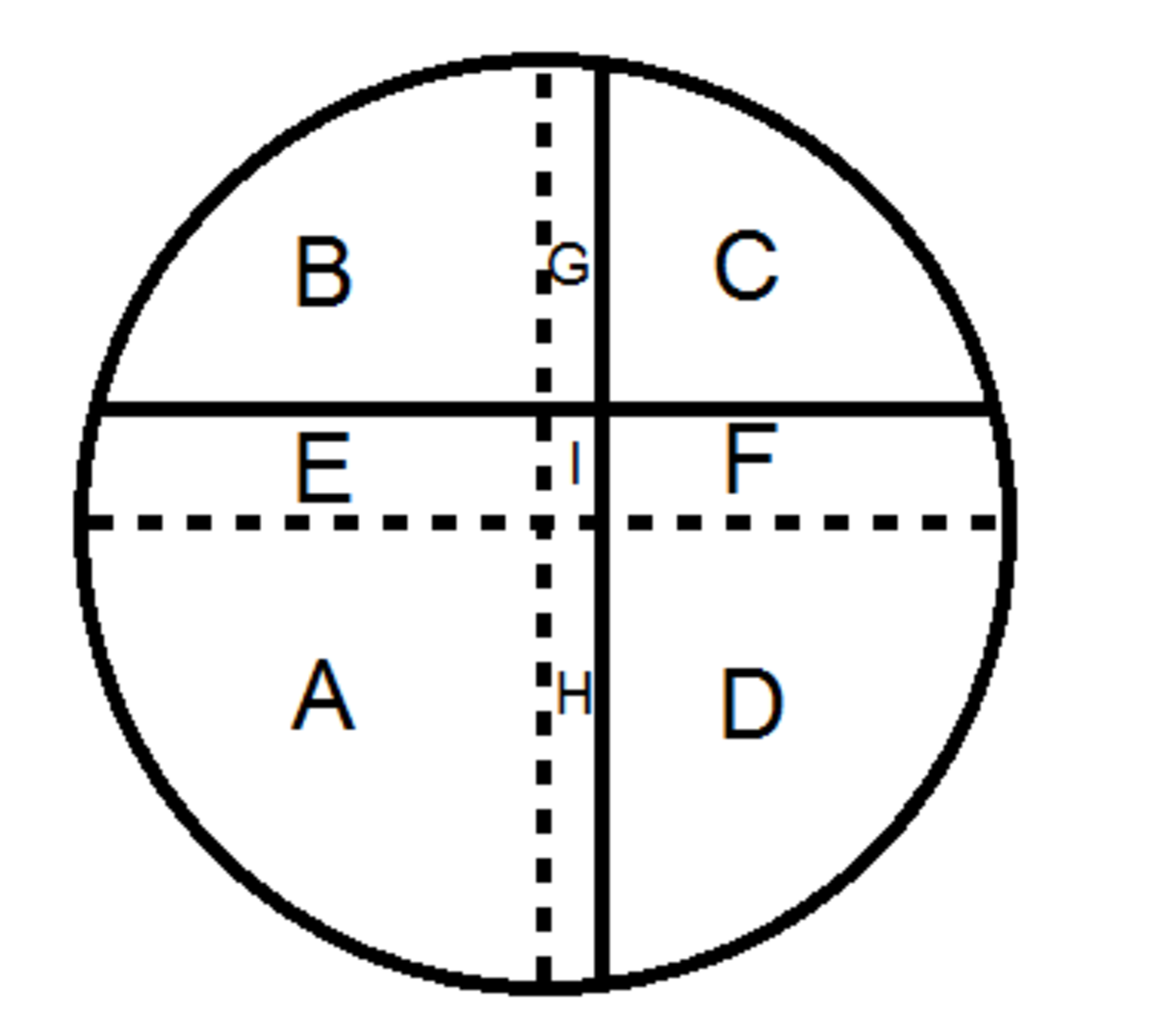
We can see that (from the figure) the following relationships E = I + F H = I + G I = ( 3 0 c m ) ( 2 2 . 5 c m ) = 6 7 5 c m 2
The area of the first quadrant and third quadrant (of the original axes) is 2 π r 2 = A + I + F + G + C
while the area of the second quadrant and fourth quadrant (of the original axes) is 2 π r 2 = B + E + D + H
Now, the shaded areas(SA) and the unshaded areas(UA) are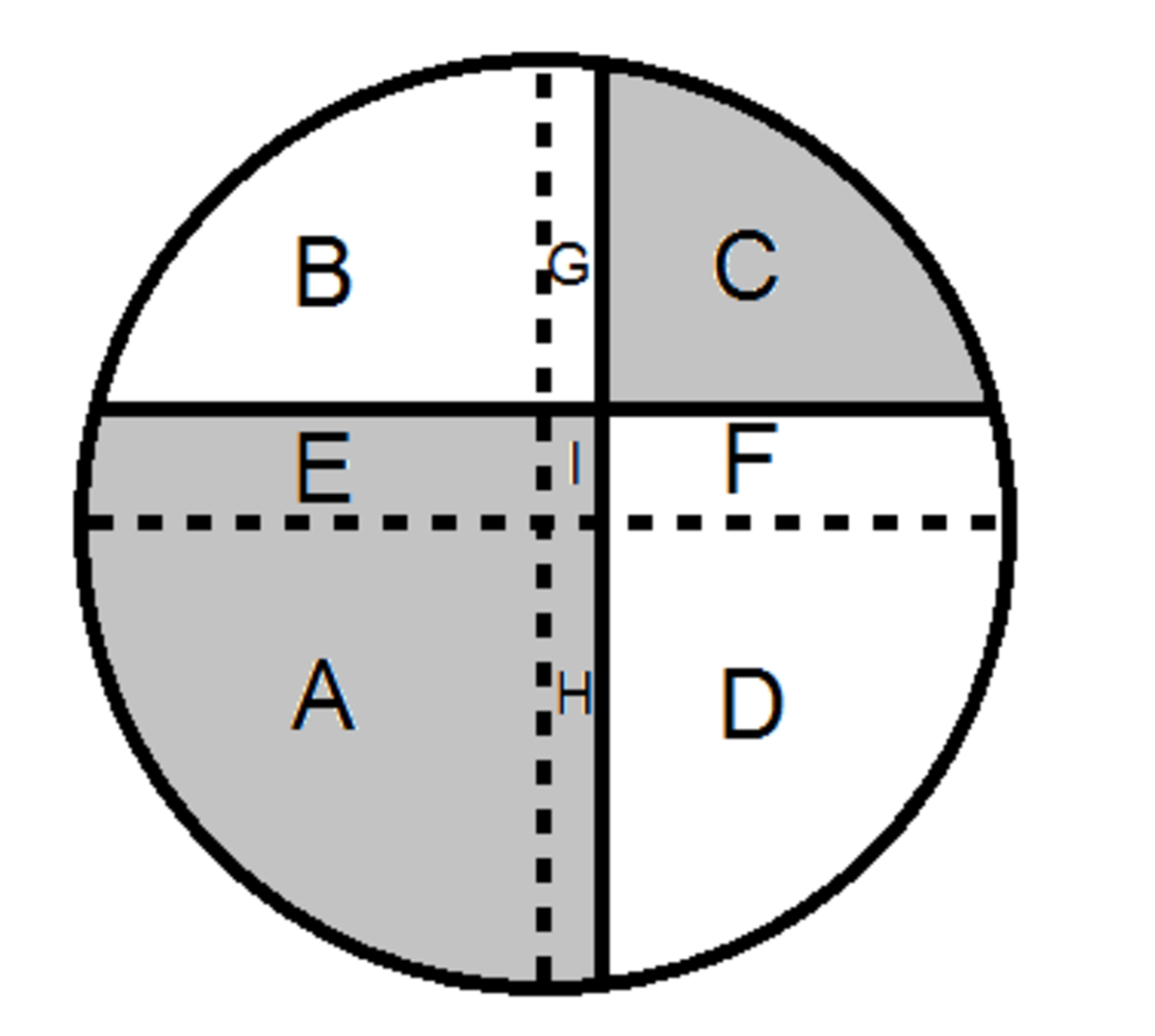 S
A
=
A
+
E
+
I
+
H
+
C
U
A
=
B
+
G
+
F
+
D
S
A
=
A
+
E
+
I
+
H
+
C
U
A
=
B
+
G
+
F
+
D
Substituting E and H in terms of I for S A while substituting F and G in terms of I for U A S A = A + F + 3 I + G + C U A = B + H + E + D − 2 I
Now substituting these equations using the previous relationships with π , then S A = 2 π r 2 + 2 I U A = 2 π r 2 − 2 I
Now take the difference between the shaded and unshaded areas. ∣ S A − U A ∣ = 4 I ∣ S A − U A ∣ = 4 ( 6 7 5 c m 2 ) ∣ S A − U A ∣ = 2 7 0 0 c m 2