2015 Countdown Problem #6: Summing Up The Years - Revisited
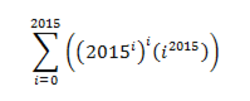 Last year I've posted the following problem
(Summing up the Years)
which has been reshared on Brilliant's official Facebook page, and this year I've decided to introduce a twist to this deceptively simple problem:
Last year I've posted the following problem
(Summing up the Years)
which has been reshared on Brilliant's official Facebook page, and this year I've decided to introduce a twist to this deceptively simple problem:
Find the last digit of i = 0 ∑ 2 0 1 5 ( ( ( 2 0 1 5 i ) i ) ( i 2 0 1 5 ) )
This problem is part of the set 2015 Countdown Problems .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The original problem is here for those who haven't seen it yet
Solution:
Note that for any integer i > 0 , the last digit of ( 2 0 1 5 ) i = the last digit of 5 i =5. Hence the last digit of ( 2 0 1 5 ) i =5, simplifying the sun to 5 ∑ i = 1 2 0 1 5 i 2 0 1 5 . It can be further simplified to 5 ∑ i = 1 2 0 1 5 ( l a s t − d i g i t − o f − i ) 2 0 1 5 .
For 0 ≤ i ≤ 9 , the last digits of i k where k is an integer are tabulated below (note the pattern):
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| x 2 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 |
| x 3 | 1 | 8 | 7 | 4 | 5 | 6 | 3 | 2 | 9 |
| x 4 | 1 | 6 | 1 | 6 | 5 | 6 | 1 | 6 | 1 |
|| x 5 || 1 || 2 || 3 || 4 || 5 || 6 || 7 || 8 || 9 ||
Note that 2015=3 (mod 4)=1 (mod 2)=5 (mod 10). Hence,
0 2 0 1 5 =0 (mod 10),
1 2 0 1 5 =1 (mod 10),
2 2 0 1 5 =2^{3 (mod 4)}=8 (mod 10),
3 2 0 1 5 =3^{3 (mod 4)}=7 (mod 10),
4 2 0 1 5 =4^{1 (mod 2)}=4 (mod 10),
5 2 0 1 5 =5 (mod 10),
6 2 0 1 5 =6 (mod 10),
7 2 0 1 5 =7^{3 (mod 4)}=3 (mod 10),
8 2 0 1 5 =8^{3 (mod 4)}=2 (mod 10), and
9 2 0 1 5 =9^{1 (mod 2)}=9 (mod 10).
Therefore, the last digit
= 5 ( 1 0 2 0 1 0 ) ( 0 + 1 + 8 + 7 + 4 + 5 + 6 + 3 + 2 + 9 ) + 5 ( 0 + 1 + 8 + 7 + 4 + 5 )
= 4 5 3 5 0 = 0 (mod 10).
For the term i = 0 , i 2 0 0 5 = 0 , so that term can be ignored. Every term other than the term we can ignore is divisible by 5.
i 2 0 1 5 is odd if and only if i is odd, and multiplying by an odd number doesn't change its parity. Therefore, every odd term is odd and all other terms are even. There are 2 2 0 1 5 + 1 = 1 0 0 8 odd terms, so their sum is even, so the entire sum is even.
Therefore the entire sum is divisible by 5 and even, so it is divisible by 10, so its last digit is 0.