#2015_3 Not that easy, huh?

$2sin\left( 1+\frac { 1 }{ 2 } +\frac { 1 }{ 4 } +\frac { 1 }{ 8 } +........+\frac { 1 }{ { 2 }^{ 2006 } } \right) 45°$ = $2sin\left( 2-\frac { 1 }{ { 2 }^{ 2006 } } \right) 45°$

= $2sin\left( 90-\frac { 45 }{ { 2 }^{ 2006 } } \right)$

= $2sin\left( \frac{\pi}{2} -\frac { \pi }{ { 4\times 2 }^{ 2006 } } \right)$

= $2cos\left( \frac { \pi }{ { 2 }^{ 2008 } } \right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad ------(1)$

Now we move to the ${ x }_{ n }$ part,

$1+cos\frac { \pi }{ 4 } \quad =\quad 2{ cos }^{ 2 }\frac { \pi }{ 8 }$

$\Rightarrow$ $2+\sqrt { 2 } =\quad 4{ cos }^{ 2 }\frac { \pi }{ 8 }$

$\Rightarrow$ ${ x }_{ 2 }=\sqrt { 2+\sqrt { 2 } } =\quad 2{ cos }\frac { \pi }{ { 2 }^{ 3 } }$

So we could form a general formula,

${ x }_{ n }=2{ cos }\frac { \pi }{ { 2 }^{ n+1 } } \quad \quad \quad \quad \quad \quad ------------(2)$

comparing (1) & (2) ,

$\Rightarrow { 2 }^{ 2008 }={ 2 }^{ n+1 }$

$\Rightarrow n=2007$

So the answer is $\boxed{{ x }_{ 2007 }}$ .

Nice problem. I solved it using induction with a spreadsheet as below:

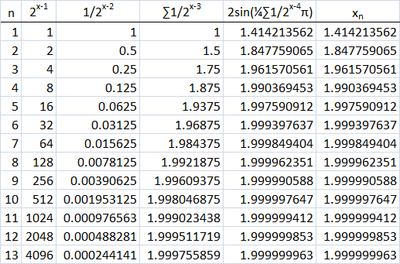
From the spreadsheet it is clear that:

$2\sin {\left( \frac {\pi}{4} \sum _{i=0} ^{n} {\frac{1}{2^i}} \right) } = x_{n+1}$

Therefore, when $n = 2006$ , then $LHS = x_{2007}$ .

In fact，we can easily find a equation as below：

2sin（1+…+1/2º）45°=2sin45°=√2=x(1)=x (0+1)

and considered that this is a CHOOSE question in the meantime，so we have a sound reason to guess that the answer is x（2006+1）=x（2007）

This is a Chinese guy's first answer，so it is an absolutely understandable thing if he has some wrong expressions. XD