When and How Do They Land?
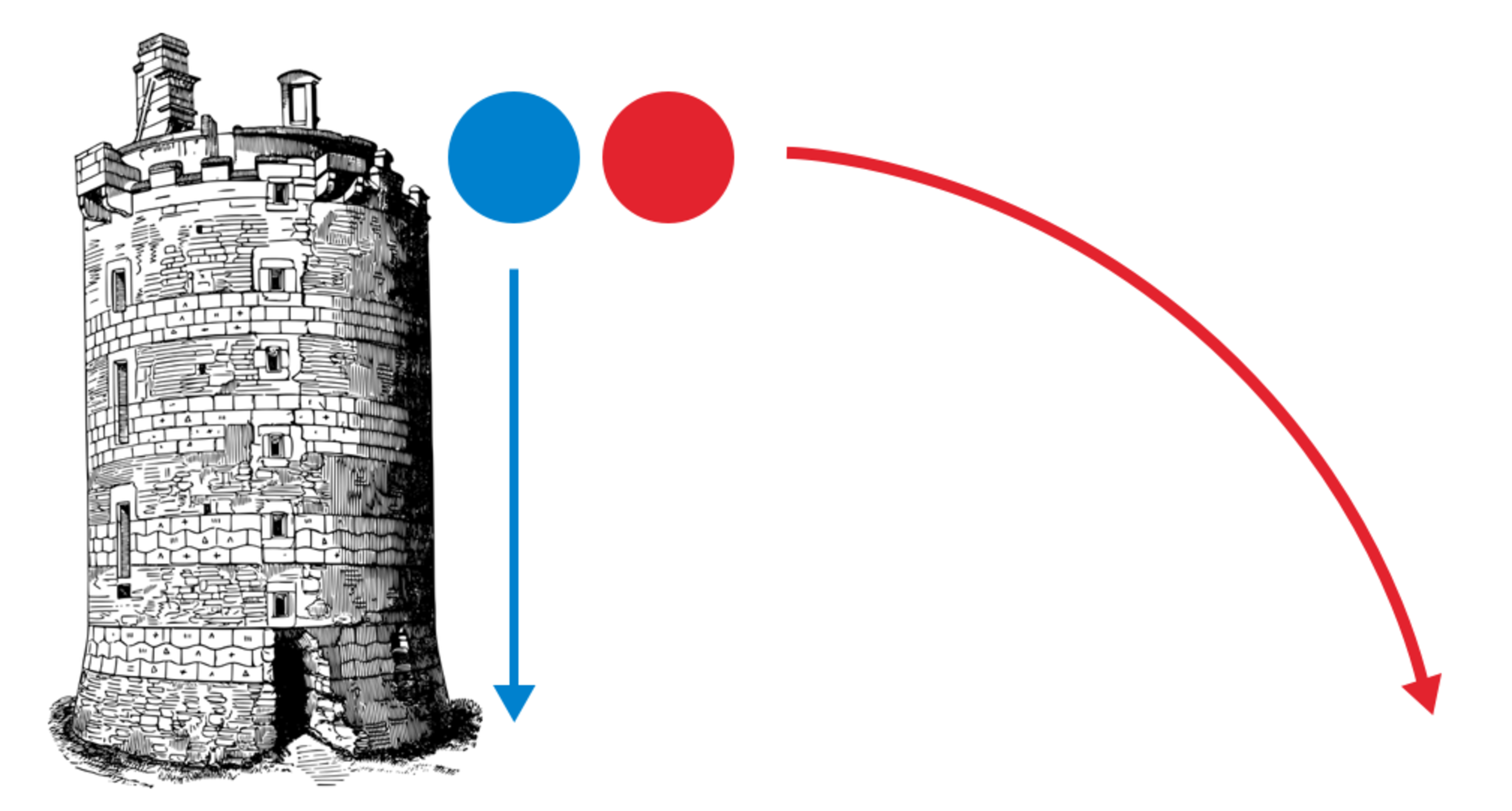
From the top of a tower, one ball is dropped and another thrown horizontally with a velocity . How will they reach the ground?
Assumptions and Details
- Neglect the rotation of the Earth.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Both situations have an initial speed, u , of 0.
But let's say that the height is 10 meters
You can use the "suvat" equations to solve for both.
For the vertical ball:
v 2 v = = = ≈ u 2 + 2 a s = 0 2 + 2 a s 2 ⋅ 9 . 8 1 ⋅ 1 0 1 4 . 0 0 m/s
And to find the time taken:
v t = = = = ≈ u + a t 0 + a t a v 1 4 / 9 . 8 1 1 . 4 3 s
For the horizontal ball,
there are 2 components therefore it is a different speed
v x 2 = u x 2 + 2 a s x horizontal component.
v y 2 = u y 2 + 2 a s y vertical component.