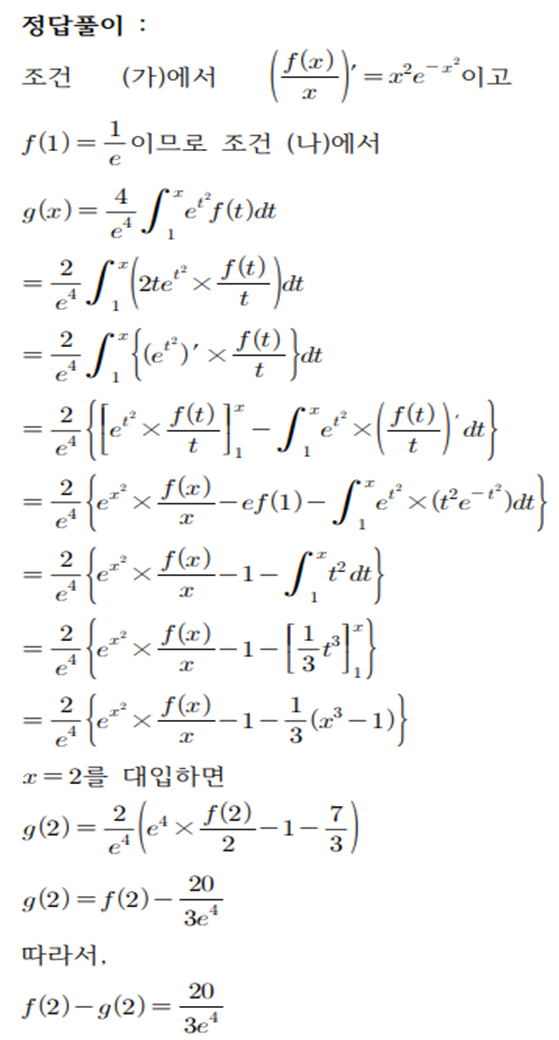2017 September Korea CSAT Mock test #21 for science&engineering students
For some function and which is differentiable in all positive real numbers, following conditions (A), (B), and (C) are true.
(A) =
(B)
(C)
calculate the value of
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Although solution is written in Korean, I suppose any math-lover would have no problem understanding this.