2018 AMC 12A Problem #17

Geometry Level 3

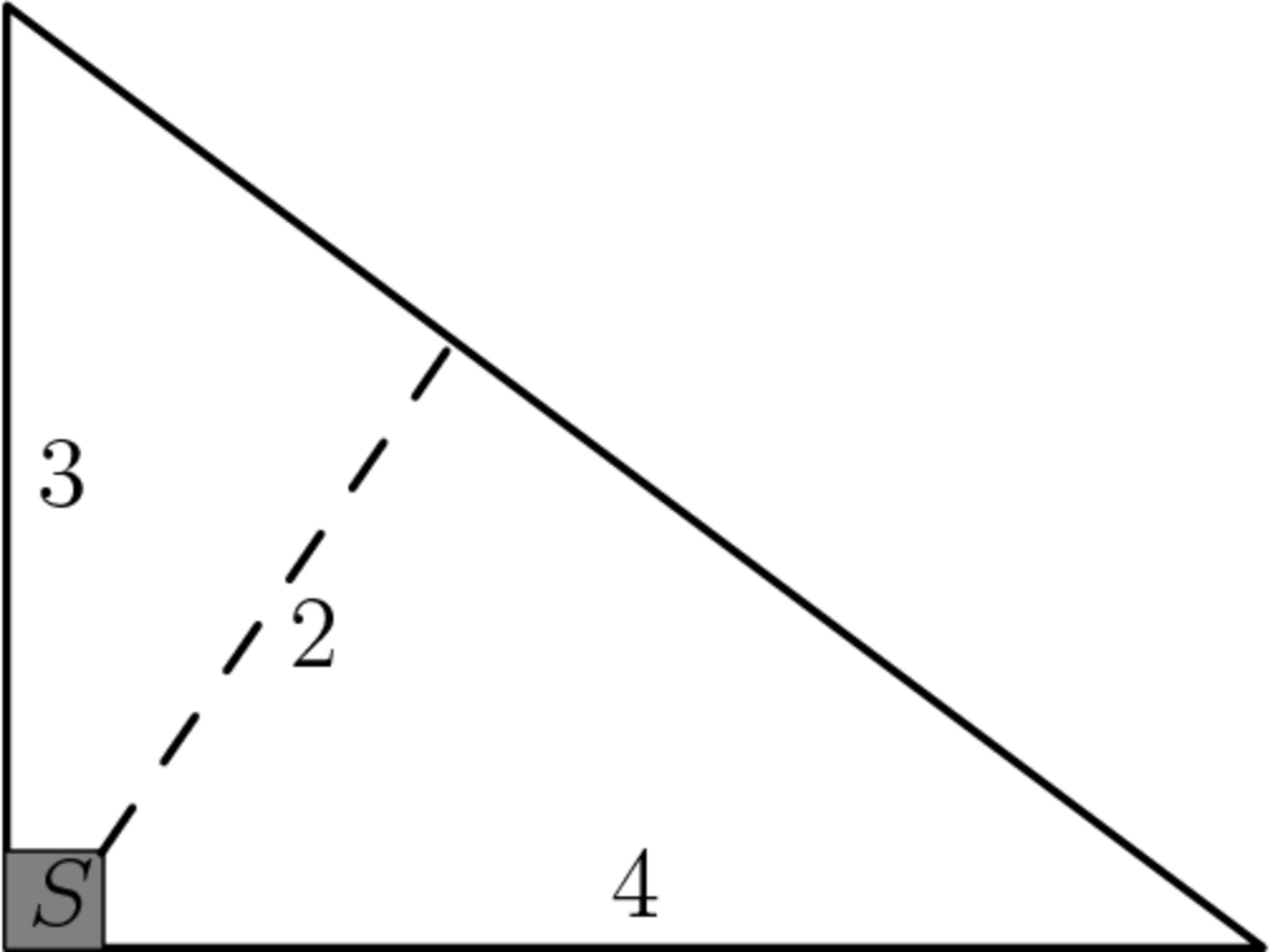
Farmer Pythagoras has a field in the shape of a right triangle. The right triangle's legs have lengths 3 and 4 units. In the corner where those sides meet at a right angle, he leaves a small unplanted square $S$ so that from the air it looks like the right angle symbol. The rest of the field is planted. The shortest distance from $S$ to the hypotenuse is 2 units. What fraction of the field is planted?

Previous problem

\dfrac{73}{75}

\dfrac{25}{27}

\dfrac{26}{27}

\dfrac{145}{147}

\dfrac{74}{75}

1 solution

Jerry McKenzie
Feb 9, 2018

Let the right angle be the origin

The hypotenuse is equated by 3x+4y=12.

Let the closest corner of S be (s,s).

The required distance is $\frac{3s+4s-12}{\sqrt{3^2+4^2}}=-2 \Rightarrow s=\frac{2}{7}$

note we use -2 as the distance because the point is under the line.

It then follows the area of the triangle is 6, the area of S is $\frac{4}{49}$ .

Thus the required fraction is $\frac{6-\frac{4}{49}}{6}=\frac{145}{147}$