2018 AMC 12A Problem #25

Number Theory Level 2

For a positive integer $n$ and nonzero digits $a,$ $b,$ and $c,$ let $A_n$ be the $n$ -digit integer each of whose digits is equal to $a$ ; let $B_n$ be the $n$ -digit integer each of whose digits is equal to $b$ ; and let $C_n$ be the $2n$ -digit (not $n$ -digit) integer each of whose digits is equal to $c.$ What is the greatest possible value of $a + b + c$ for which there are at least two values of $n$ such that $C_n - B_n = A_n^2$ ?

Previous problem

All problems

18 12 20 16 14

1 solution

Haosen Chen
Feb 8, 2018

Express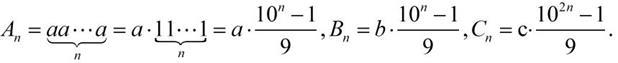 Then 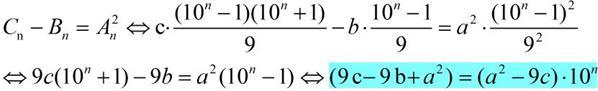Now,remember there are at least two values of n satisfying the equality above,which leads to 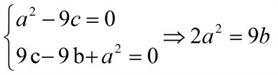It means a=3 or 6, since 3 is a divisor of a and 9b≤81 . a=3 gives b=2,c=1; a=6 gives b=8,c=4. Thus (a+b+c)max =18

2018 AMC 12A Problem #25

1 solution

0 pending reports