A Colorful Problem
At the zoo, there is an exhibition filled with a rare breed of chameleons. This breed consists of red, blue, and green variants. In that exhibition, 15 of the chameleons are red, 13 are blue, and 17 are green. If two chameleons of two different colors meet, they will both turn into the third color.
- If a red chameleon meets a green chameleon, both chameleons will turn blue.
- If a blue chameleon meets a green chameleon, both chameleons will turn red.
- If a red chameleon meets a blue chameleon, both chameleons will turn green.
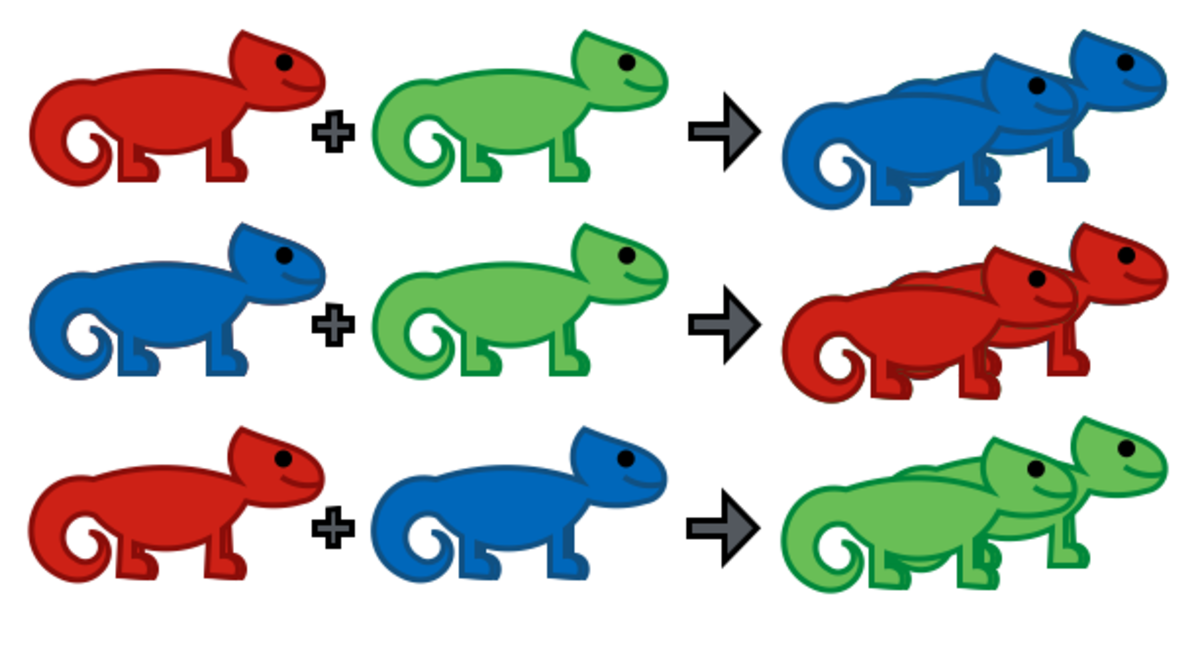
Is it possible for all of the chameleons to become a single color?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let R n , B n , G n be the respective number of red, blue and green chameleons after n chameleon "meetings". If two chameleons of the same color meet then R n + 1 = R n , B n + 1 = B n and G n + 1 = G n . If two chameleons of different colors meet, then the values change as follows:
(i) red meets blue: R n + 1 = R n − 1 , B n + 1 = B n − 1 , G n + 1 = G n + 2
(ii) red meets green: R n + 1 = R n − 1 , B n + 1 = B n + 2 , G n + 1 = G n − 1
(iii) blue meets green: R n + 1 = R n + 2 , B n + 1 = B n − 1 , G n + 1 = G n − 1
Now note that in each of these cases,
R n + 1 − B n + 1 ≡ R n − B n ( m o d 3 )
R n + 1 − G n + 1 ≡ R n − G n ( m o d 3 )
B n + 1 − G n + 1 ≡ B n − G n ( m o d 3 )
In other words, the pairwise modulo 3 differences between the numbers of chameleons of different colors is invariant, and in particular are the same as they are at the start of the process. So with R 0 = 1 5 , B 0 = 1 3 , G 0 = 1 7 , we have that for any n , R n − B n ≡ 2 ( m o d 3 ) , R n − G n ≡ 1 ( m o d 3 ) and B n − G n ≡ 2 ( m o d 3 ) .
But if at some point all the chameleons were the same color, say R = 4 5 , then B − G = 0 − 0 ≡ 0 ( m o d 3 ) , which is impossible since we must always have B n − G n ≡ 2 ( m o d 3 ) . Similarly for B = 4 5 and G = 4 5 . Thus it is impossible for all the chameleons to simultaneously be the same color.