Number Carousel

Let the sum is $4k$ as it is multiple of four.

There will four equations whose each sum is $4k$ .Let each number in the circle of outer side is $c_i$ where $1\leq i \leq 8$ and center circle is $c$

So, adding the four equations $\displaystyle \sum_{i=1}^{8} c_i +4c=4k \times 4=16k \\ (1+2+3+...+9) + 3c=16k \\ 45+3c=16k \\ 3(c+15)=16k \\$

So, $16| c+15$ .The only possible value is $c=1$

Therefore, the value in the center square is $\boxed{1}$

Now , using this value we get $k=3$ So, each sum is $4 \times3=12$ .The sum of two opposite square is $12-1=11$ .The pairs are

$\{(9,2);(8,3);(6,5);(4,7)\}$

So, we get the whole arrangement.

There are several different ways to fill in the above diagram. In all cases, the white center circle must have the number 1, while the other 8 are split into pairs all adding up to 11. This means that on any one line, the sum of three numbers would be 12.

We can figure this out if we consider the fact that the sum of the numbers 1 to 9 equals 45. Knowing that, now we must find a number which we can subtract from 45 to get a multiple of 4. That means the only possible candidates for the center number are 1, 5, and 9.

We first test the number 9. Subtracting 9 from 45 gives you 36, and since we're dealing with 4 pairs of equal sums, we divide 36 by 4 to get 9. The only possible way to get a multiple of 4 up to this point is if we add 3 onto 9. The only way we can make the number 3 using two unique digits is 1 + 2. Therefore, the number 9 can't be the center number.

Next, we test the number 5. Subtracting 5 from 45 gives you 40, and we divide 40 by 4 to get 10. To get a multiple of 4, we add 2 onto 10. But we have already stated that 5 is our center number, so we can't use 5 as the center number.

Finally, if we test the number 1, by subtracting 1 from 45, we get 44, and then divide 44 by 4 to get 11. To get a multiple of 4, we add 1 onto 11. To get the number 11, the possible sums consisting of only digits are $2 + 9$ , $3 + 8$ , $4 + 7$ , and $5 + 6$ . A possible diagram to represent this would look like this:

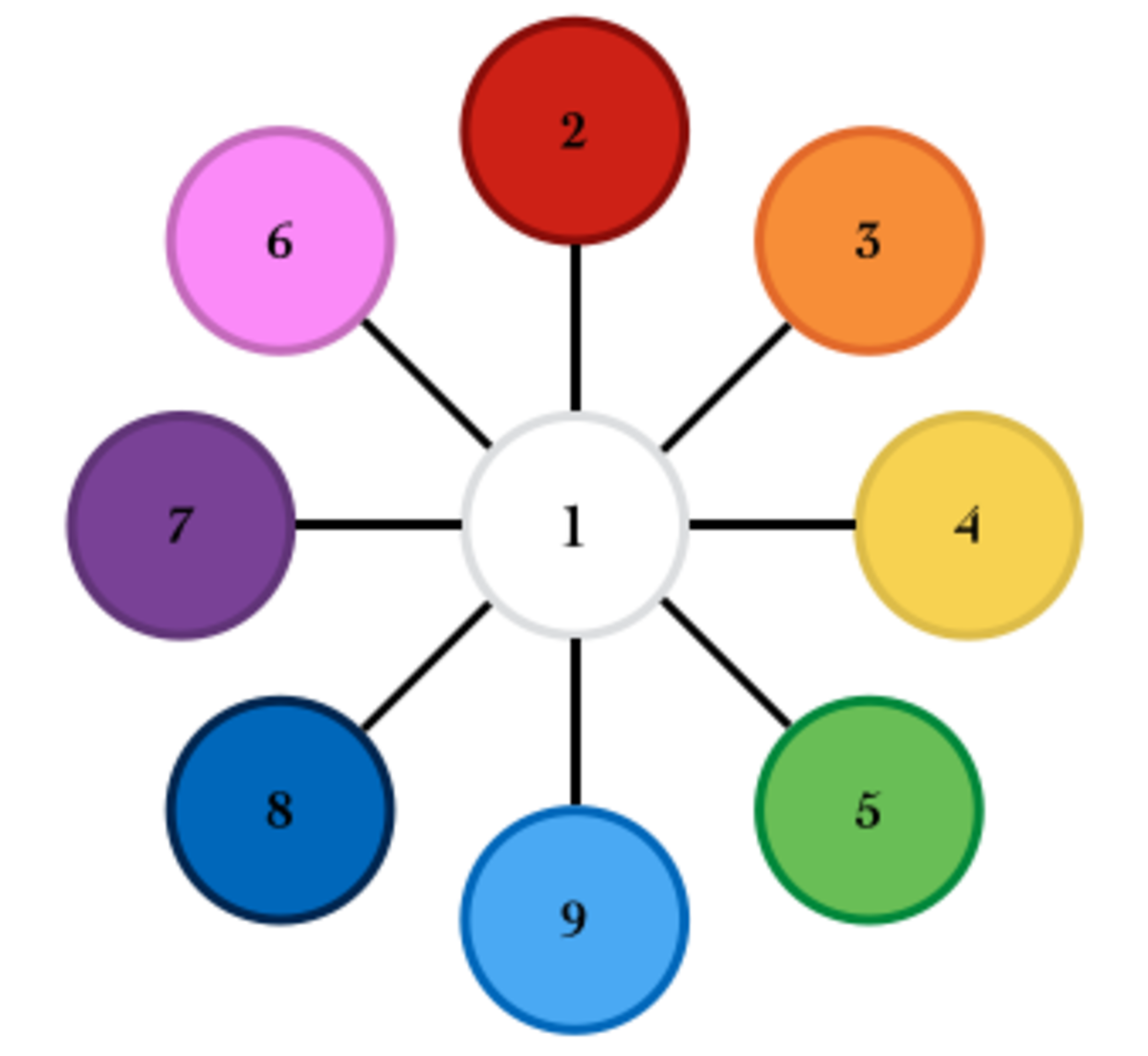
Hence, $\boxed{1}$ should be the center number.